Question

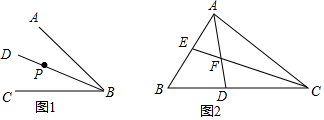
12．如图1，已知BD是∠ABC平分线，P是角平分线上任意一点．作图：以B为圆心，任意长为半径画弧，分别BA交于点E，交BC于点F，联结PE，PF，则△BEP和△BFP关于直线BD对称，（保留作图痕迹） 
用符号语言将这对全等的三角形表示为△BEP≌△BFP．
利用这种方法解答：
如图2，在△ABC中，∠B=60°，AD、CE分别平分∠BAC、∠ACB，AD与CE相交于F．求证：FE=FD．

Answer 1

分析 直接利用角平分线的性质结合全等三角形的判定与性质分别得出答案．

解答 解：如图1所示：则△BEP和△BFP关于直线BD对称，（保留作图痕迹） 
用符号语言将这对全等的三角形表示为△BEP≌△BFP．
故答案为：BEP，BFP；BEP，BFP；

如图2，在AC上截取AG=AE，联结FG，
在△AEF和△AGF中，
$\left\{\begin{array}{l}{AE=AG}\\{∠EAF=∠FAG}\\{AF=AF}\end{array}\right.$，
∴△AEF≌△AGF（SAS），
∴∠AFE=∠AFG，FE=FG，
∵∠B=60°，AD、CE分别平分∠BAC、∠ACB，
可得∠FAC+∠FCA=60°，
∴∠AFE=∠AFG=∠CFD=60°，∠CFG=60°，
在△CGF和△CDF中
$\left\{\begin{array}{l}{∠GFC=∠DFC}\\{FC=FC}\\{∠GCF=∠FCD}\end{array}\right.$，
∴△CGF≌△CDF（ASA），
∴FD=FG，
综上可得EF=FD．

点评 此题主要考查了复杂作图以及全等三角形的判定与性质，正确掌握全等三角形的判定方法是解题关键．