题目内容
6.正方形ABCD的一条对角线AC长为4,则它的边长是2$\sqrt{2}$,面积是8.分析 由正方形的性质知:△ABC是等腰直角三角形,已知了斜边AC的长,即可求得直角边AB、BC的值,也就求得了正方形的边长,进而可求出其面积.
解答 解:∵四边形ABCD为正方形,
∴AB=BC,∠ABC=90°,
故AC=$\sqrt{2}$AB,
即AB=$\frac{1}{\sqrt{2}}$AC=2$\sqrt{2}$,
故正方形的面积S=a2=8,
所以此题的答案为:2$\sqrt{2}$,8.
点评 本题考查了勾股定理的运用以及正方形的性质,解题的关键是将图形转化到等腰直角三角形中求解.对正方形的性质需有充分认识.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
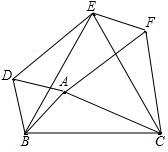 如图,以△ABC的三边为边,在BC的同侧作三个等边△ABD,△BEC,△ACF
如图,以△ABC的三边为边,在BC的同侧作三个等边△ABD,△BEC,△ACF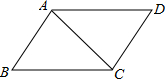 已知?ABCD的周长是16cm,△ABC的周长是14cm,求AC的长.
已知?ABCD的周长是16cm,△ABC的周长是14cm,求AC的长. 如图,在△ABC和△ABD中,AC=AD,若利用“HL”证明△ABC≌△ABD,则需要加条件∠C=∠D=90°,.
如图,在△ABC和△ABD中,AC=AD,若利用“HL”证明△ABC≌△ABD,则需要加条件∠C=∠D=90°,. 如图是一个正方体的表面展开图,相对面上两个数互为相反数,则x+y=-6.
如图是一个正方体的表面展开图,相对面上两个数互为相反数,则x+y=-6. 如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F点处,已知AD=10cm,BF=6cm,求图中阴影部分的面积.
如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F点处,已知AD=10cm,BF=6cm,求图中阴影部分的面积.