题目内容
6.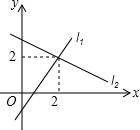 如图,直线l1:y=k1x+b1与直线l2:y=k2x+b2交于点(2,2),则方程组$\left\{\begin{array}{l}{y={k}_{1}x+{b}_{1}}\\{y={k}_{2}x+{b}_{2}}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$.
如图,直线l1:y=k1x+b1与直线l2:y=k2x+b2交于点(2,2),则方程组$\left\{\begin{array}{l}{y={k}_{1}x+{b}_{1}}\\{y={k}_{2}x+{b}_{2}}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$.
分析 根据任何一个一次函数都可以化为一个二元一次方程,再根据两个函数交点坐标就是二元一次方程组的解可直接得到答案.
解答 解:∵直线l1:y=k1x+b1与直线l2:y=k2x+b2交于点(2,2),
∴二元一次方程组$\left\{\begin{array}{l}{y={k}_{1}x+{b}_{1}}\\{y={k}_{2}x+{b}_{2}}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$,
故答案为:$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$
点评 本题主要考查了函数解析式与图象的关系,满足解析式的点就在函数的图象上,在函数的图象上的点,就一定满足函数解析式.函数图象交点坐标为两函数解析式组成的方程组的解.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
15.一枚硬币抛向空中,落地时正面朝上的概率是( )
| A. | 0 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
16.若-5x2ym与xny是同类项,则方程nx-m=7的解是( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |

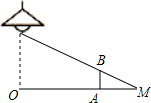 如图,身高1.6米的小明站在距离灯的底部(点O)20米的A处,经测量小明的影子AM长为5米,则路灯的高度为8米.
如图,身高1.6米的小明站在距离灯的底部(点O)20米的A处,经测量小明的影子AM长为5米,则路灯的高度为8米. 如图,直线AB、CD相交于点O,OE是∠AOC的角平分线,且∠DOE=5∠COE,求∠AOC的度数.
如图,直线AB、CD相交于点O,OE是∠AOC的角平分线,且∠DOE=5∠COE,求∠AOC的度数.