题目内容
18.计算:(1)-3×2+(-3)÷(-$\frac{1}{2}$);
(2)(-2)3×($\frac{1}{2}$-$\frac{3}{4}$-$\frac{5}{8}$);
(3)-24-$\frac{1}{5}$×(4-18×$\frac{1}{2}$).
分析 (1)原式先计算乘除运算,再计算加减运算即可得到结果;
(2)原式先计算乘方运算,再利用乘法分配律计算即可得到结果;
(3)原式先计算乘方运算,再计算乘法运算,最后算加减运算即可得到结果.
解答 解:(1)原式=-6+6=0;
(2)原式=-4+6+5=7;
(3)原式=-16+1=-15.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
8. 数轴上有A、B、C、D四个点,其中绝对值等于2的点是( )
数轴上有A、B、C、D四个点,其中绝对值等于2的点是( )
 数轴上有A、B、C、D四个点,其中绝对值等于2的点是( )
数轴上有A、B、C、D四个点,其中绝对值等于2的点是( )| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
13.一件衬衫先按成本加价60元标价,再以8折出售,仍可获利24元,这件衬衫的成本是多少钱?设衬衫的成本为x元.
(1)填写下表:(用含有x的代数式表示)
(2)根据相等关系列出方程:(0.8x+48)-x=24.
(1)填写下表:(用含有x的代数式表示)
| 成本 | 标价 | 售价 |
| x | x+60 | 0.8x+48 |
3.下表中的字母都是按移动规律排列的.
我们把某格中的字母的和所得多项式称为特征多项式,例如第1格的“特征多项式”为6x+2y,第2格的“特征多项式”为9x+4y,回答下列问题.
(1)第3格的“特征多项式”为12x+6y,第4格的“特征多项式”为15x+8y,第n格的“特征多项式”为3(n+1)x+2ny(n为正整数);
(2)求第6格的“特征多项式”与第5格的“特征多项式”的差.
| 序号 | 1 | 2 | 3 | … |
图形 | x x y x x y x x | x x x y y x x x y y x x x | x x x x y y y x x x x y y y x x x x | … |
(1)第3格的“特征多项式”为12x+6y,第4格的“特征多项式”为15x+8y,第n格的“特征多项式”为3(n+1)x+2ny(n为正整数);
(2)求第6格的“特征多项式”与第5格的“特征多项式”的差.
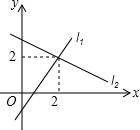 如图,直线l1:y=k1x+b1与直线l2:y=k2x+b2交于点(2,2),则方程组$\left\{\begin{array}{l}{y={k}_{1}x+{b}_{1}}\\{y={k}_{2}x+{b}_{2}}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$.
如图,直线l1:y=k1x+b1与直线l2:y=k2x+b2交于点(2,2),则方程组$\left\{\begin{array}{l}{y={k}_{1}x+{b}_{1}}\\{y={k}_{2}x+{b}_{2}}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$.