题目内容
16.有一个计算程序,每次运算这种运算的过程如下:
则第n次运算的结果yn$\frac{{2}^{n}x}{({2}^{n}-1)x+1}$.(用含有x和n的式子表示)
分析 把y1代入确定出y2,依此类推得到一般性规律,即可确定出第n次运算结果.
解答 解:把y1=$\frac{2x}{x+1}$代入得:y2=$\frac{2•\frac{2x}{x+1}}{\frac{2x}{x+1}+1}$=$\frac{4x}{3x+1}$,
把y2=$\frac{4x}{3x+1}$代入得:y3=$\frac{2•\frac{4x}{3x+1}}{\frac{4x}{3x+1}+1}$=$\frac{8x}{7x+1}$,
依此类推,得到yn=$\frac{{2}^{n}x}{({2}^{n}-1)x+1}$,
故答案为:$\frac{{2}^{n}x}{({2}^{n}-1)x+1}$
点评 此题考查了分式的混合运算,弄清题中的规律是解本题的关键.

练习册系列答案
相关题目
11.目前我国年可利用的淡水资源总量为27500亿立方米,人均占有量居全世界第110位,因此我们要节约用水,27500亿这个数用科学记数法表示为( )
| A. | 2.75×1013 | B. | 2.75×1012 | C. | 2.75×1011 | D. | 2.75×1010 |
8. 数轴上有A、B、C、D四个点,其中绝对值等于2的点是( )
数轴上有A、B、C、D四个点,其中绝对值等于2的点是( )
 数轴上有A、B、C、D四个点,其中绝对值等于2的点是( )
数轴上有A、B、C、D四个点,其中绝对值等于2的点是( )| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
 有增根,则m的值为____________.
有增根,则m的值为____________. 有个零件(正方体中间挖去一个圆柱形孔)如图放置,它的左视图是( )
有个零件(正方体中间挖去一个圆柱形孔)如图放置,它的左视图是( )



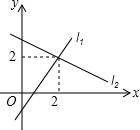 如图,直线l1:y=k1x+b1与直线l2:y=k2x+b2交于点(2,2),则方程组$\left\{\begin{array}{l}{y={k}_{1}x+{b}_{1}}\\{y={k}_{2}x+{b}_{2}}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$.
如图,直线l1:y=k1x+b1与直线l2:y=k2x+b2交于点(2,2),则方程组$\left\{\begin{array}{l}{y={k}_{1}x+{b}_{1}}\\{y={k}_{2}x+{b}_{2}}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$.