题目内容
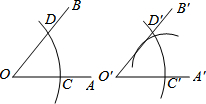请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图，请你根据图形全等的知识，说明画出∠A′O′B′=∠AOB的依据是（ ）| A、SSS | B、SAS |
| C、ASA | D、AAS |
考点：作图—基本作图,全等三角形的判定
专题：
分析：根据作图过程可知O′C′=OC，O′D′=OD，C′D′=CD，所以运用的是三边对应相等，两三角形全等作为依据．
解答：解：根据作图过程可知O′C′=OC，O′D′=OD，C′D′=CD，
在△OCD与△O′C′D′中，
∴△OCD≌△O′C′D′（SSS），
∴∠A′O′B′=∠AOB．
故选：A．
在△OCD与△O′C′D′中，
|
∴△OCD≌△O′C′D′（SSS），
∴∠A′O′B′=∠AOB．
故选：A．
点评：本题考查基本作图“作一个角等于已知角”的相关知识，其理论依据是三角形全等的判定“边边边”定理和全等三角形对应角相等．从作法中找已知，根据已知条件选择判定方法．
练习册系列答案
相关题目
如图，在矩形ABCD中，对角线AC、BD相交于点G，连结BE交AC于F，连结FD．若∠BFA=90°，AB=3，tan∠ACB=
如图，直线AB与EF相交于点M，∠EMB=88°，∠1=60°．要使AB∥CD，则将直线AB绕点M逆时针旋转的度数为（ ）| A、28° | B、30° |
| C、60° | D、88° |
如图，已知点P（x，y）在第一象限，且x+y=8，点A的坐标是（6，0），如果设△OPA的面积是s，则s与x之间的函数关系式是（ ）| A、s=-3x+24 |
| B、s=3x+24 |
| C、s=3x |
| D、s=-3x |
下列说法中正确的是（ ）
| A、如果a＞b，则ac2＞bc2（c≠0） |
| B、如果ax＞-a，则x＞-1 |
| C、如果a＜b，则-2a＜-2b |
| D、如果a＜b，则a-b＞0 |