题目内容
在△ABC中,∠B=45°,∠C=30°,AB=
,则AC= .
| 2 |
考点:勾股定理,含30度角的直角三角形,等腰直角三角形
专题:
分析:如图,过A点作AD⊥BC于D点,把一般三角形转化为两个直角三角形,然后分别在两个直角三角形中利用三角函数,即可求出AC的长度.
解答: 解:过A点作AD⊥BC于D点;
解:过A点作AD⊥BC于D点;
在直角三角形ABD中,∠B=45°,AB=
,
则AD=AB•sin∠B=1,
在直角三角形ADC中,∠C=30°,
则AC=2AD=2.
故答案为:2.
 解:过A点作AD⊥BC于D点;
解:过A点作AD⊥BC于D点;在直角三角形ABD中,∠B=45°,AB=
| 2 |
则AD=AB•sin∠B=1,
在直角三角形ADC中,∠C=30°,
则AC=2AD=2.
故答案为:2.
点评:考查了勾股定理,解答此类题目的关键是要通过作辅助线把三角关系转化成直角三角形的问题求解.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
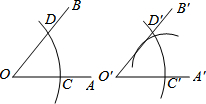 请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图,请你根据图形全等的知识,说明画出∠A′O′B′=∠AOB的依据是( )
请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图,请你根据图形全等的知识,说明画出∠A′O′B′=∠AOB的依据是( )| A、SSS | B、SAS |
| C、ASA | D、AAS |
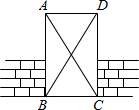 如图,工人师傅砌门时,要想检验门框ABCD是否符合设计要求(即门框是否为矩形),在确保两组对边分别平行的前提下,只要测量出对角线AC、BD的长度,然后看它们是否相等就可判断了.
如图,工人师傅砌门时,要想检验门框ABCD是否符合设计要求(即门框是否为矩形),在确保两组对边分别平行的前提下,只要测量出对角线AC、BD的长度,然后看它们是否相等就可判断了.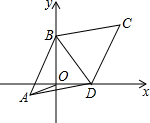 如图,已知菱形ABCD中,BC=10,∠BCD=60°两顶点B、D分别在平面直角坐标系的y轴、x轴的正半轴上滑动,连接OA,则OA的长的最小值是
如图,已知菱形ABCD中,BC=10,∠BCD=60°两顶点B、D分别在平面直角坐标系的y轴、x轴的正半轴上滑动,连接OA,则OA的长的最小值是