题目内容
如图，直线AB与EF相交于点M，∠EMB=88°，∠1=60°．要使AB∥CD，则将直线AB绕点M逆时针旋转的度数为（ ）| A、28° | B、30° |
| C、60° | D、88° |
考点：平行线的判定
专题：
分析：根据同位角相等，两直线平行进行判断．
解答：解：要使AB∥CD，则∠EMB=∠1=60°，
而∠EMB=88°，
所以直线AB绕点M逆时针旋转的度数=88°-60°=28°．
故选A．
而∠EMB=88°，
所以直线AB绕点M逆时针旋转的度数=88°-60°=28°．
故选A．
点评：本题考查了平行线的判定：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行．
练习册系列答案
相关题目
如图，△ABC的面积为12，BD=2DC，AE=EC，那么阴影部分的面积是
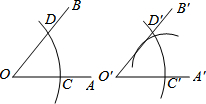请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图，请你根据图形全等的知识，说明画出∠A′O′B′=∠AOB的依据是（ ）| A、SSS | B、SAS |
| C、ASA | D、AAS |
如图，△ABC内接于⊙O，∠A=60°，BC=4| 3 |
 |
| BC |
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
计算（a+1）（-a+1）的结果是（ ）
| A、a2-1 |
| B、-a2-1 |
| C、1-a2 |
| D、-a2-2a-1 |
下列不是同类项的是（ ）
A、-2与
| ||
| B、2m与2n | ||
C、-
| ||
D、-x2y2与
|
已知圆锥的母线为10，高为8，则此圆锥的侧面积是（ ）
| A、24π | B、30π |
| C、48π | D、60π |