题目内容
若抛物线y=x2+bx+c的对称轴为x=2,顶点与x轴距离为5,则b= ,c= .
考点:待定系数法求二次函数解析式
专题:
分析:根据二次函数的顶点坐标公式求出b、c的值即可.
解答:解:∵抛物线y=x2+bx+c的对称轴为x=2,顶点与x轴距离为5,
∴抛物线y=x2+bx+c的顶点为(2,5)或(2,-5),
∴-
=2,即-
=2,解得b=-4;
=±5,即
=±5,解得c=9或c=1.
故答案为:-4;9或1.
∴抛物线y=x2+bx+c的顶点为(2,5)或(2,-5),
∴-
| b |
| 2a |
| b |
| 2×1 |
| 4ac-b2 |
| 4a |
| 4c-(-4)2 |
| 4×1 |
故答案为:-4;9或1.
点评:本题考查的是二次函数的性质,熟知二次函数y=ax2+bx+c的顶点坐标为(-
,
)是解答此题的关键.
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
相关题目
 (1)在平面直角坐标系中,描出下列4个点:A(-1,0),B(3,0),C(2,2),顺次连接A,B,C,组成三角形ABC;
(1)在平面直角坐标系中,描出下列4个点:A(-1,0),B(3,0),C(2,2),顺次连接A,B,C,组成三角形ABC;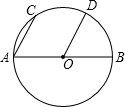 如图,AB是⊙O的直径,OD∥AC,
如图,AB是⊙O的直径,OD∥AC,
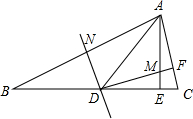 如图,在△ABC中,AE⊥BC于点E,∠B=22.5°,AB的垂直平分线DN交BC于点D,交AB于点N,DF⊥AC于点F,交AE于点M,求证:EM=EC.
如图,在△ABC中,AE⊥BC于点E,∠B=22.5°,AB的垂直平分线DN交BC于点D,交AB于点N,DF⊥AC于点F,交AE于点M,求证:EM=EC.
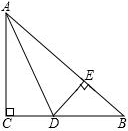 如图,在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E.
如图,在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E. 如图,在半径为5的⊙O中,AB是直径,弦CD⊥AB,弦AD=
如图,在半径为5的⊙O中,AB是直径,弦CD⊥AB,弦AD=