题目内容
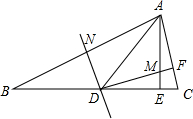 如图,在△ABC中,AE⊥BC于点E,∠B=22.5°,AB的垂直平分线DN交BC于点D,交AB于点N,DF⊥AC于点F,交AE于点M,求证:EM=EC.
如图,在△ABC中,AE⊥BC于点E,∠B=22.5°,AB的垂直平分线DN交BC于点D,交AB于点N,DF⊥AC于点F,交AE于点M,求证:EM=EC.考点:线段垂直平分线的性质
专题:证明题
分析:先根据线段垂直平分线的性质得出AD=BD,由三角形外角的性质得出∠ADE的度数,判断出△ADE的形状,再由ASAA定理得出△DEM≌△AEC,由此可得出结论.
解答:证明:AB的垂直平分线DN交BC于点D,
∴BD=AD,
∴∠B=∠BAD=22.5,
∴∠ADE=2∠B=45°.
∵AE⊥BC于E,
∴△ADE是等腰直角三角形,
∴DE=AE.
∵DF⊥AC于F交AE于M,
∴∠DEM=∠AEC=90°,
∵∠EDM+∠C=∠CAE+∠C=90°
∴∠EDM=∠EAC
在△DEM与△AEC中,
∵
,
∴△DEM≌△AEC(ASA),
∴EM=EC.
∴BD=AD,
∴∠B=∠BAD=22.5,
∴∠ADE=2∠B=45°.
∵AE⊥BC于E,
∴△ADE是等腰直角三角形,
∴DE=AE.
∵DF⊥AC于F交AE于M,
∴∠DEM=∠AEC=90°,
∵∠EDM+∠C=∠CAE+∠C=90°
∴∠EDM=∠EAC
在△DEM与△AEC中,
∵
|
∴△DEM≌△AEC(ASA),
∴EM=EC.
点评:本题考查的是线段垂直平分线的性质,熟知线段垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 在数轴上,a,b,c三点的位置如图所示,则|a+c|+|b-c|+|a-b|=
在数轴上,a,b,c三点的位置如图所示,则|a+c|+|b-c|+|a-b|= 如图,过点P分别画OA,OB的平行线交OA于点E,交OB于点F,并且用量角器量出∠PEO,∠PFO,∠AOB的大小,找找它们有哪些关系.
如图,过点P分别画OA,OB的平行线交OA于点E,交OB于点F,并且用量角器量出∠PEO,∠PFO,∠AOB的大小,找找它们有哪些关系.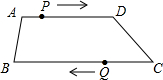 如图,在四边形ABCD中,AD∥BC,AD=24cm,BC=30cm,点P自点A向点D以3cm/s的速度运动,到点D即停止,点Q自点C向点B以2cm/s的速度运动,到点B即停止,直线PQ截这个四边形为两个四边形,问:当P,Q同时出发,几秒后其中一个四边形为平行四边形?
如图,在四边形ABCD中,AD∥BC,AD=24cm,BC=30cm,点P自点A向点D以3cm/s的速度运动,到点D即停止,点Q自点C向点B以2cm/s的速度运动,到点B即停止,直线PQ截这个四边形为两个四边形,问:当P,Q同时出发,几秒后其中一个四边形为平行四边形? 如图,试表示到点P的距离等于2.5cm的点的集合.
如图,试表示到点P的距离等于2.5cm的点的集合.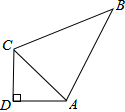 如图,四边形ABCD中,AB=13,BC=12,CD=3,AD=4,若∠D=90°,求△ABC的面积.
如图,四边形ABCD中,AB=13,BC=12,CD=3,AD=4,若∠D=90°,求△ABC的面积.