题目内容
 如图,在半径为5的⊙O中,AB是直径,弦CD⊥AB,弦AD=2
如图,在半径为5的⊙O中,AB是直径,弦CD⊥AB,弦AD=2| 5 |
考点:圆周角定理,解直角三角形
专题:
分析:连接BD,根据圆周角定理得出∠ADB=90°.再由垂径定理得出
=
,故∠ABD=∠ADC,根据勾股定理求出BD的长,进而可得出结论.
 |
| AC |
 |
| AD |
解答: 解:连接BD,
解:连接BD,
∵AB是直径,
∴∠ADB=90°.
∵CD⊥AB,
∴
=
,
∴∠ABD=∠ADC,
在Rt△ADB中,
∵AB=10,AD=2
,
∴BD=
=
=4
,
∴cos∠ADC=cos∠B=
=
=
.
 解:连接BD,
解:连接BD,∵AB是直径,
∴∠ADB=90°.
∵CD⊥AB,
∴
 |
| AC |
 |
| AD |
∴∠ABD=∠ADC,
在Rt△ADB中,
∵AB=10,AD=2
| 5 |
∴BD=
| AB2-AD2 |
102-(2
|
| 5 |
∴cos∠ADC=cos∠B=
| BD |
| AB |
4
| ||
| 10 |
2
| ||
| 5 |
点评:本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,从电线杆离地面15m的A点处向地面拉一条长17m的钢索电线杆,这条钢索在地面的固定点B距离电线杆底部C点有多远?
如图,从电线杆离地面15m的A点处向地面拉一条长17m的钢索电线杆,这条钢索在地面的固定点B距离电线杆底部C点有多远?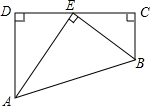 如图,四边形ABCD中,∠D=∠C=90°,点E在CD上,AE平分∠DAB,BE平分∠CBA,若AD=4,AB=6,则CB的长为( )
如图,四边形ABCD中,∠D=∠C=90°,点E在CD上,AE平分∠DAB,BE平分∠CBA,若AD=4,AB=6,则CB的长为( )
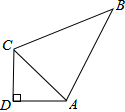 如图,四边形ABCD中,AB=13,BC=12,CD=3,AD=4,若∠D=90°,求△ABC的面积.
如图,四边形ABCD中,AB=13,BC=12,CD=3,AD=4,若∠D=90°,求△ABC的面积.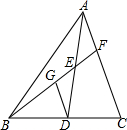 如图,在△ABC中,AD是BC边上的中线,E是AD的中点,连接BE并延长交AC于点F,DG是△BCF的中位线,求证:AF=
如图,在△ABC中,AD是BC边上的中线,E是AD的中点,连接BE并延长交AC于点F,DG是△BCF的中位线,求证:AF=