题目内容
17.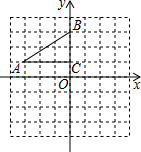 如图,在平面直角坐标系中,直角△ABC的三个顶点分别是A(-3,1),B(0,3),C(0,1)
如图,在平面直角坐标系中,直角△ABC的三个顶点分别是A(-3,1),B(0,3),C(0,1)(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C1;
(2)分别连结AB1、BA1后,求四边形AB1A1B的面积.
分析 (1)利用网格特点,延长AC到A1使A1C=AC,延长BC到B1使B1C=BC,C点的对应点C1与C点重合,则△A1B1C1满足条件;
(2)四边形AB1A1B的对角线互相垂直平分,则四边形AB1A1B为菱形,然后利用菱形的面积公式计算即可.
解答 解:(1)如图,△A1B1C1为所作,
(2)四边形AB1A1B的面积=$\frac{1}{2}$×6×4=12.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.

练习册系列答案
相关题目
7.下列各数中比0小的数是( )
| A. | -2 | B. | 1$\frac{1}{3}$ | C. | 3 | D. | $\sqrt{3}$ |
8. 如图,抛物线y=x2-2x-3与x轴交于点A、D,与y轴交于点C,四边形ABCD是平行四边形,则点B的坐标是( )
如图,抛物线y=x2-2x-3与x轴交于点A、D,与y轴交于点C,四边形ABCD是平行四边形,则点B的坐标是( )
 如图,抛物线y=x2-2x-3与x轴交于点A、D,与y轴交于点C,四边形ABCD是平行四边形,则点B的坐标是( )
如图,抛物线y=x2-2x-3与x轴交于点A、D,与y轴交于点C,四边形ABCD是平行四边形,则点B的坐标是( )| A. | (-4,-3) | B. | (-3,-3) | C. | (-3,-4) | D. | (-4,-4) |
2. 象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“車”的点的坐标为(-2,1),棋子“炮”的点的坐标为(1,3),则表示棋子“馬”的点的坐标为( )
象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“車”的点的坐标为(-2,1),棋子“炮”的点的坐标为(1,3),则表示棋子“馬”的点的坐标为( )
 象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“車”的点的坐标为(-2,1),棋子“炮”的点的坐标为(1,3),则表示棋子“馬”的点的坐标为( )
象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“車”的点的坐标为(-2,1),棋子“炮”的点的坐标为(1,3),则表示棋子“馬”的点的坐标为( )| A. | (-4,3) | B. | (3,4) | C. | (-3,4) | D. | (4,3) |
9.一物体及其主视图如图所示,则它的左视图与俯视图分别是下列图形中的( )


| A. | ①④ | B. | ①③ | C. | ②④ | D. | ②③ |
7.已知△ABC∽△DEF,若△ABC与△DEF的相似比为$\frac{3}{4}$,则△ABC与△DEF对应中线的比为( )
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{9}{16}$ | D. | $\frac{16}{9}$ |
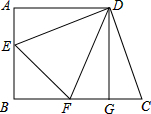 如图,正方形ABGD中,AB=AD=6,梯形ABCD中,DE⊥DC交AB于E,DF平分∠EDC交BC于F,连结EF.
如图,正方形ABGD中,AB=AD=6,梯形ABCD中,DE⊥DC交AB于E,DF平分∠EDC交BC于F,连结EF.