题目内容
6.(1)计算:(-3)2-($\frac{1}{5}$)-1-$\sqrt{8}$×$\sqrt{2}$+(-2)0(2)先化简,再求值:$\frac{2{x}^{2}-2x}{{x}^{2}-1}$-$\frac{x}{x+1}$,其中x=-2.
分析 (1)根据实数的运算顺序,首先计算乘方和乘法,然后从左到右依次计算,求出算式(-3)2-($\frac{1}{5}$)-1-$\sqrt{8}$×$\sqrt{2}$+(-2)0的值是多少即可.
(2)先把$\frac{2{x}^{2}-2x}{{x}^{2}-1}$-$\frac{x}{x+1}$化简为最简分式,再把x=-2代入求值即可.
解答 解:(1)(-3)2-($\frac{1}{5}$)-1-$\sqrt{8}$×$\sqrt{2}$+(-2)0
=9-5-4+1
=1
(2)x=-2时,
$\frac{2{x}^{2}-2x}{{x}^{2}-1}$-$\frac{x}{x+1}$
=$\frac{2x(x-1)}{(x+1)(x-1)}$-$\frac{x}{x+1}$
=$\frac{2x}{x+1}$-$\frac{x}{x+1}$
=$\frac{x}{x+1}$
=$\frac{-2}{-2+1}$
=2
点评 (1)此题主要考查了实数的运算,要熟练掌握,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到右的顺序进行.另外,有理数的运算律在实数范围内仍然适用.
(2)此题还考查了零指数幂的运算,要熟练掌握,解答此题的关键是要明确:①a0=1(a≠0);②00≠1.
(3)此题还考查了分式的化简求值,要熟练掌握,解答此题的关键是要明确:一般是先化简为最简分式或整式,再代入求值.化简时不能跨度太大,而缺少必要的步骤.
(4)此题还考查了负整数指数幂的运算,要熟练掌握,解答此题的关键是要明确:①a-p=$\frac{1}{{a}^{p}}$(a≠0,p为正整数);②计算负整数指数幂时,一定要根据负整数指数幂的意义计算;③当底数是分数时,只要把分子、分母颠倒,负指数就可变为正指数.

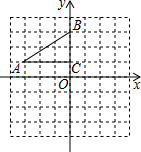 如图,在平面直角坐标系中,直角△ABC的三个顶点分别是A(-3,1),B(0,3),C(0,1)
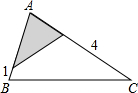
如图,在平面直角坐标系中,直角△ABC的三个顶点分别是A(-3,1),B(0,3),C(0,1)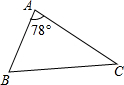 如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )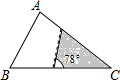

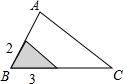
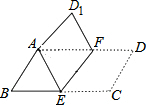 如图,把平行四边形ABCD折叠,使点C与点A重合,这时点D落在D1,折痕为EF,若∠BAE=55°,则∠D1AD=55°.
如图,把平行四边形ABCD折叠,使点C与点A重合,这时点D落在D1,折痕为EF,若∠BAE=55°,则∠D1AD=55°.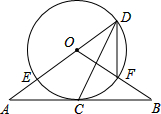 如图,直线AB经过⊙O上的点C,直线AO与⊙O交于点E和点D,OB与⊙O交于点F,连接DF、DC.已知OA=OB,CA=CB,DE=10,DF=6.
如图,直线AB经过⊙O上的点C,直线AO与⊙O交于点E和点D,OB与⊙O交于点F,连接DF、DC.已知OA=OB,CA=CB,DE=10,DF=6. 如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论:
如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论: