题目内容
19.在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在直线DC,CB上移动.(1)如图①,当点E自D向C,点F自C向B移动时,连接AE和DF交于点P,请你写出AE与DF的关系,并说明理由.
(2)如图②,当点E,F分别移动到边DC,CB的延长线上时,连接AE和DF,(1)中的结论还成立吗?(请你直接作答,不需证明)
(3)如图③,当E,F分别在边CD,BC的延长线上移动时,连接AE和DF,(1)中的结论还成立吗?请说明理由.
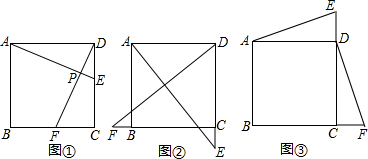
分析 (1)AE=DF,AE⊥DF.先证得△ADE≌△DCF.由全等三角形的性质得AE=DF,∠DAE=∠CDF,再由等角的余角相等可得AE⊥DF;
(2)由正方形的性质得出AD=DC,∠ADE=∠DCF=90°,DE=CF,SAS证出△ADE≌△DCF,得出AE=DF,∠DAE=∠CDF,证出∠DAE+∠ADF=90°,得出AE⊥DF;
(3)成立.由(1)同理可证AE=DF,∠DAE=∠CDF,延长FD交AE于点G,再由等角的余角相等可得AE⊥DF.
解答 解:(1)AE=DF,AE⊥DF;理由如下:
∵四边形ABCD是正方形,
∴AD=DC,∠ADC=∠C=90°,
∵动点E,F分别从D,C两点同时出发,以相同的速度在直线DC,CB上移动,
∴DE=CF,
在△ADE和△DCF中,
$\left\{\begin{array}{l}{AD=DC}\\{∠ADC=∠C}\\{DE=CF}\end{array}\right.$,
∴△ADE≌△DCF(SAS),
∴AE=DF,∠DAE=∠CDF,
由于∠CDF+∠ADF=90°,
∴∠DAE+∠ADF=90°,
∴∠APD=90°,
∴AE⊥DF;
(2)成立;理由如下:
∵四边形ABCD是正方形,
∴AD=DC,∠ADC=∠DCF=90°,
∵动点E,F分别从D,C两点同时出发,以相同的速度在直线DC,CB上移动,
∴DE=CF,
在△ADE和△DCF中,
$\left\{\begin{array}{l}{AD=DC}\\{∠ADC=∠DCF}\\{DE=CF}\end{array}\right.$,
∴△ADE≌△DCF(SAS),
∴AE=DF,∠DAE=∠CDF,
由于∠CDF+∠ADF=90°,
∴∠DAE+∠ADF=90°,
∴AE⊥DF;
(3)成立;理由如下: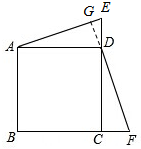 同(1)得:AE=DF,∠DAE=∠CDF,
同(1)得:AE=DF,∠DAE=∠CDF,
延长FD交AE于点G,如图所示:
则∠CDF+∠ADG=90°,
∴∠ADG+∠DAE=90°,
∴∠AGD=90°,
∴AE⊥DF.
点评 本题是四边形综合题目,考查了正方形的性质、全等三角形的判定与性质、互余两角的关系、垂线的证法等知识;本题难度较大,综合性强,熟练掌握正方形的性质,证明三角形全等是解决问题的关键.

 优加精卷系列答案
优加精卷系列答案| A. | a$\sqrt{x}$-b$\sqrt{y}$ | B. | b$\sqrt{x}$-a$\sqrt{y}$ | C. | $\sqrt{y}$-$\sqrt{x}$ | D. | $\sqrt{y}$+$\sqrt{x}$ |
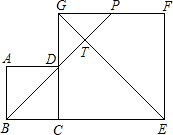 如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交EG于点T,交FG于点P,则GT的长为2$\sqrt{2}$.
如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交EG于点T,交FG于点P,则GT的长为2$\sqrt{2}$.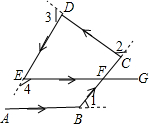 如图,汽车沿“A→B→C→D→E→F”前进过程中,经过四次转弯后与原来方向相同,四次转完的角度分别为∠1、∠2、∠3、∠4,求∠1+∠2+∠3+∠4的度数.
如图,汽车沿“A→B→C→D→E→F”前进过程中,经过四次转弯后与原来方向相同,四次转完的角度分别为∠1、∠2、∠3、∠4,求∠1+∠2+∠3+∠4的度数. 如图所示,有五个大小相同的正方形拼成“T“字形,试将它分成四块全等的图形.
如图所示,有五个大小相同的正方形拼成“T“字形,试将它分成四块全等的图形. 如图,△ABC中,∠ABC的外角平分线BD与∠ACB外角平分线CE相交于点P,求证:点P到三边AB、BC、CA所在直线的距离相等.
如图,△ABC中,∠ABC的外角平分线BD与∠ACB外角平分线CE相交于点P,求证:点P到三边AB、BC、CA所在直线的距离相等.