题目内容
8.若等式(2x-4)2+|y-$\frac{1}{2}$|=0中的x,y满足方程mx+4y=8和5x+16y=n,求2m2-n+$\frac{1}{4}$mn的值.分析 根据平方与绝对值为非负数,得到2x-4=0,y-$\frac{1}{2}$=0,求出x,y的值,再分别代入方程mx+4y=8和5x+16y=n,求出m,n的值,即可解答.
解答 解:∵等式(2x-4)2+|y-$\frac{1}{2}$|=0,
∴$\left\{\begin{array}{l}{2x-4=0}\\{y-\frac{1}{2}=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=2}\\{y=\frac{1}{2}}\end{array}\right.$,
把$\left\{\begin{array}{l}{x=2}\\{y=\frac{1}{2}}\end{array}\right.$代入方程mx+4y=8和5x+16y=n,得,2m+2=8,10+8=n,
解得:m=3,n=18,
把m=3,n=18,代入2m2-n+$\frac{1}{4}$mn得:
$2×{3}^{2}-18+\frac{1}{4}×3×18$=$\frac{27}{2}$.
点评 本题考查了二元一次方程的解,解决本题的关键是根据平方与绝对值为非负数,得到2x-4=0,y-$\frac{1}{2}$=0.

练习册系列答案
相关题目
18.大于-2且小于3的正整数有( )个.
| A. | 1 | B. | 2 | C. | 4 | D. | 4 |
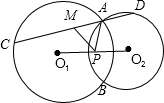 设圆O1,圆O2交于点A,B,过A作直线CD交圆O1,圆O2于C,D,M为CD的中点,P为O1O2的中点.求证:PM=PA.
设圆O1,圆O2交于点A,B,过A作直线CD交圆O1,圆O2于C,D,M为CD的中点,P为O1O2的中点.求证:PM=PA.