题目内容
 如图所示,AD∥CE,CD⊥CF,CD平分∠ACE,且∠1=∠2,试问BF与AD平行吗?为什么?
如图所示,AD∥CE,CD⊥CF,CD平分∠ACE,且∠1=∠2,试问BF与AD平行吗?为什么?考点:平行线的判定与性质
专题:
分析:由角平分线的性质可结合条件∠ECF=∠1,可证明BF∥CE,则有BF∥AD.
解答:解:平行,理由如下:
∵CD平分∠ACE,
∴∠ACD=∠DCE,
∵CD⊥CF,
∴∠DCF=90°,
∴∠DCE+∠ECF=90°,且∠DCA+∠1=90°,
∴∠ECF=∠1,
∵∠1=∠2,
∴∠ECF=∠2,
∴CE∥BF,
又AD∥CE,
∴BF∥AD.
∵CD平分∠ACE,
∴∠ACD=∠DCE,
∵CD⊥CF,
∴∠DCF=90°,
∴∠DCE+∠ECF=90°,且∠DCA+∠1=90°,
∴∠ECF=∠1,
∵∠1=∠2,
∴∠ECF=∠2,
∴CE∥BF,
又AD∥CE,
∴BF∥AD.
点评:本题主要考查平行线的性质和判定,掌握平行线的性质和判定是解题的关键,即①两直线平行?同位角相等,②两直线平行?内错角相等,③两直线平行?同旁内角互补,④a∥b,b∥c?a∥c.

练习册系列答案
相关题目
 如图,程程和小磊在他们家附近的公园中玩跷跷板,跷跷板上的横板AD通过点B,且可以绕点B上下转动,木桩BC与路面AC始终成90°,当处在如图所示的位置时∠ABC=60°,则这个跷跷板上下最多可以转动( )
如图,程程和小磊在他们家附近的公园中玩跷跷板,跷跷板上的横板AD通过点B,且可以绕点B上下转动,木桩BC与路面AC始终成90°,当处在如图所示的位置时∠ABC=60°,则这个跷跷板上下最多可以转动( )| A、180° | B、120° |
| C、90° | D、60° |
 如图,在△ABC中,∠A=45°,∠B=30°,CD⊥AB,垂足为D,BC=3,则AD的长为( )
如图,在△ABC中,∠A=45°,∠B=30°,CD⊥AB,垂足为D,BC=3,则AD的长为( )| A、2 | ||
| B、1.5 | ||
| C、1 | ||
D、
|
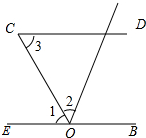 已知,∠1=∠2,∠2=∠3.求证:CD∥EB.
已知,∠1=∠2,∠2=∠3.求证:CD∥EB. 已知,如图,△ABC中,∠C=90°,D是AB上一点,DE⊥CD于D,交BC于E,且有AC=AD=CE,求证:DE=
已知,如图,△ABC中,∠C=90°,D是AB上一点,DE⊥CD于D,交BC于E,且有AC=AD=CE,求证:DE= 如图,AB是半圆O的直径,C为半圆上一点,过C作半圆的切线,连接AC,作直线AD,使∠DAC=∠CAB,AD交半圆于E,交过C点的切线于点D.
如图,AB是半圆O的直径,C为半圆上一点,过C作半圆的切线,连接AC,作直线AD,使∠DAC=∠CAB,AD交半圆于E,交过C点的切线于点D. 如图,某人在一个建筑物AM的顶部A观察另一个建筑物BN的顶部B的仰角为α,如果建筑物AM的高度为56米,两建筑物间的间距为MN为48米,
如图,某人在一个建筑物AM的顶部A观察另一个建筑物BN的顶部B的仰角为α,如果建筑物AM的高度为56米,两建筑物间的间距为MN为48米, 为了了解某校500名七年级新生入学时的数学水平,随机抽取若干名学生的数学成绩统计整理后绘制如图的频数分布直方图,观察图形回答下列问题:
为了了解某校500名七年级新生入学时的数学水平,随机抽取若干名学生的数学成绩统计整理后绘制如图的频数分布直方图,观察图形回答下列问题: