题目内容
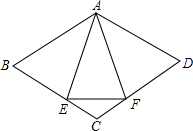 已知:如图,菱形ABCD中,E、F分别是CB、CD上的点,∠BAF=∠DAE.
已知:如图,菱形ABCD中,E、F分别是CB、CD上的点,∠BAF=∠DAE.(1)求证:AE=AF;
(2)若AE垂直平分BC,AF垂直平分CD,求证:△AEF为等边三角形.
考点:菱形的性质,全等三角形的判定与性质,等边三角形的判定
专题:证明题
分析:(1)首先利用菱形的性质得出AB=AD,∠B=∠D,进而得出△ABE≌△ADF(ASA),即可得出答案;
(2)利用垂直平分线的性质得出△ABC和△ACD都是等边三角形,进而得出∠EAF=∠CAE+∠CAF=60°,求出△AEF为等边三角形.
(2)利用垂直平分线的性质得出△ABC和△ACD都是等边三角形,进而得出∠EAF=∠CAE+∠CAF=60°,求出△AEF为等边三角形.
解答:(1) 证明:∵四边形ABCD是菱形,
证明:∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D,
又∵∠BAF=∠DAE,
∴∠BAE=∠DAF,
在△ABE和△ADF中,
,
∴△ABE≌△ADF(ASA),
∴AE=AF;
(2)解:连接AC,
∵AE垂直平分BC,AF垂直平分CD,
∴AB=AC=AD,
∵AB=BC=CD=DA,
∴△ABC和△ACD都是等边三角形,
∴∠CAE=∠BAE=30°,∠CAF=∠DAF=30°,
∴∠EAF=∠CAE+∠CAF=60°,
又∵AE=AF,
∴△AEF是等边三角形.
 证明:∵四边形ABCD是菱形,
证明:∵四边形ABCD是菱形,∴AB=AD,∠B=∠D,
又∵∠BAF=∠DAE,
∴∠BAE=∠DAF,
在△ABE和△ADF中,
|
∴△ABE≌△ADF(ASA),
∴AE=AF;
(2)解:连接AC,
∵AE垂直平分BC,AF垂直平分CD,
∴AB=AC=AD,
∵AB=BC=CD=DA,
∴△ABC和△ACD都是等边三角形,
∴∠CAE=∠BAE=30°,∠CAF=∠DAF=30°,
∴∠EAF=∠CAE+∠CAF=60°,
又∵AE=AF,
∴△AEF是等边三角形.
点评:此题主要考查了等边三角形的判定与性质以及全等三角形的判定与性质等知识,熟练掌握全等三角形的判定方法是解题关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
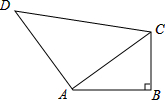 如图,∠B=90°,AB=4cm,BC=3cm,AD=12cm,CD=13cm,求四边形ABCD的面积.
如图,∠B=90°,AB=4cm,BC=3cm,AD=12cm,CD=13cm,求四边形ABCD的面积.
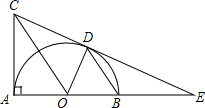 如图,已知BD是以O为圆心,AB长为直径的半圆的弦,AC⊥AB,BD∥OC,直线CD交AB的延长线于点E.
如图,已知BD是以O为圆心,AB长为直径的半圆的弦,AC⊥AB,BD∥OC,直线CD交AB的延长线于点E.