题目内容
1. 将正整数按如图所示的规律排列下去.若用有序实数对(n,m)表示第n排,从左到右第m个数,如(4,3)表示实数9,则2020可用有序实数对表示为(64,4).
将正整数按如图所示的规律排列下去.若用有序实数对(n,m)表示第n排,从左到右第m个数,如(4,3)表示实数9,则2020可用有序实数对表示为(64,4).
分析 根据第n排有n个数字,且从左到右逐渐增大知第n排最后一个数字为1+2+3+…+n=$\frac{n(n+1)}{2}$,求出n=63时的值可知第63排最后一个数字的为2016,从而得出2020的位置.
解答 解:由题意知,第n排有n个数字,且从左到右逐渐增大,
则第n排最后一个数字为1+2+3+…+n=$\frac{n(n+1)}{2}$,
当n=63时,$\frac{n(n+1)}{2}$=$\frac{63×64}{2}$=2016,
即第63排最后一个数字的为2016,
∴2020位于第64排第4个数,
则2020可用有序实数对表示为(64,4),
故答案为:(64,4).
点评 本题主要考查数字的变化类,根据题意得出第n排有n个数字,且从左到右逐渐增大得出第n排的最后一个数字是解题的关键.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
11.“滴滴打车”深受大众欢迎,该打车方式的总费用由里程费和耗时费组成,其中里程费按p元/千米计算,耗时费按q元/分钟计算.小明、小亮两人用该打车方式出行,按上述计价规则,其打车总费用、行驶里程数与车速如表:
(1)求p,q的值;
(2)“滴滴”推出新政策,在原有付费基础上,当里程数超过8千米后,超出的部分要加收0.6元/千米的里程费.某天,小丽两次使用“滴滴打车”共花费52元,总里程20千米,已知两次“滴滴打车”行驶的平均速度为40千米/小时,求小丽第一次“滴滴打车”的里程数?
| 时间(分钟) | 里程数(千米) | 车费(元) | |
| 小明 | 7 | 5 | 12.1 |
| 小亮 | 6 | 4.5 | 10.8 |
(2)“滴滴”推出新政策,在原有付费基础上,当里程数超过8千米后,超出的部分要加收0.6元/千米的里程费.某天,小丽两次使用“滴滴打车”共花费52元,总里程20千米,已知两次“滴滴打车”行驶的平均速度为40千米/小时,求小丽第一次“滴滴打车”的里程数?
6.一次函数y=kx+b不经过第二象限,则( )
| A. | k>0,b<0 | B. | k>0,b≤0 | C. | k<0,b<0 | D. | k<0,b≤0 |
13.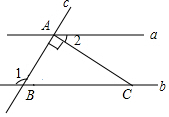 如图,平行直线a,b被直线c所截,分别相交于点A,B,过点A作AC⊥AB,交直线于点C.若∠1=128°,则∠2的度数是( )
如图,平行直线a,b被直线c所截,分别相交于点A,B,过点A作AC⊥AB,交直线于点C.若∠1=128°,则∠2的度数是( )
 如图,平行直线a,b被直线c所截,分别相交于点A,B,过点A作AC⊥AB,交直线于点C.若∠1=128°,则∠2的度数是( )
如图,平行直线a,b被直线c所截,分别相交于点A,B,过点A作AC⊥AB,交直线于点C.若∠1=128°,则∠2的度数是( )| A. | 128° | B. | 90° | C. | 52° | D. | 38° |
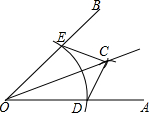 如图,已知∠AOB,以O为圆心,以任意长为半径画弧,分别交OA、OB于D,E两点,再分别以D,E为圆心,大于 $\frac{1}{2}$DE长为半径画弧,两条弧交于点C,作射线OC,则△OEC≌△ODC的依据是SSS.
如图,已知∠AOB,以O为圆心,以任意长为半径画弧,分别交OA、OB于D,E两点,再分别以D,E为圆心,大于 $\frac{1}{2}$DE长为半径画弧,两条弧交于点C,作射线OC,则△OEC≌△ODC的依据是SSS.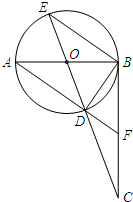 如图,AB是⊙O的直径,BC⊥AB,垂足为点B,连接CO并延长交⊙O于点D、E,连接AD并延长交BC于点F,则下列结论正确的有( )
如图,AB是⊙O的直径,BC⊥AB,垂足为点B,连接CO并延长交⊙O于点D、E,连接AD并延长交BC于点F,则下列结论正确的有( )
 把下面的直线补充成一条数轴,然后在数轴上标出下列各数,并用“>”连接各数.
把下面的直线补充成一条数轴,然后在数轴上标出下列各数,并用“>”连接各数.