题目内容
20.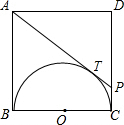 如图,在正方形ABCD中,以BC边为直径作半圆O,AP切半圆O于T点,交CD于P点,求AT:TP的值.
如图,在正方形ABCD中,以BC边为直径作半圆O,AP切半圆O于T点,交CD于P点,求AT:TP的值.
分析 设CP=PT=x,AB=AT=y,在△APD中根据勾股定理可得列方程,求出y=4x,即可得出答案.
解答 解:∵四边形ABCD是正方形,
∴AD=DC=BC=AB,∠D=90°,∠DCB=∠ABC=90°,
∴AB切⊙O于B,DC切⊙O于C,
根据切线长定理得:CP=PT,AB=AT,
设CP=PT=x,AB=AT=y,
则在直角△APD中,DP=y-x,AD=CD=y,AP=x+y,
根据勾股定理可得:
(y-x)2+y2=(x+y)2,
∴y=4x,
∴$\frac{AT}{TP}$=$\frac{4x}{x}$=4.
点评 此题考查圆的切线长定理,正方形的性质和勾股定理等知识,解答本题关键是运用切线长定理得出CP=PT,AB=AT,从而求解.

练习册系列答案
相关题目
11.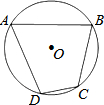 如图,四边形ABCD是⊙O的内接四边形,若∠DAB=64°,则∠BCD的度数是( )
如图,四边形ABCD是⊙O的内接四边形,若∠DAB=64°,则∠BCD的度数是( )
 如图,四边形ABCD是⊙O的内接四边形,若∠DAB=64°,则∠BCD的度数是( )
如图,四边形ABCD是⊙O的内接四边形,若∠DAB=64°,则∠BCD的度数是( )| A. | 64° | B. | 90° | C. | 136° | D. | 116° |
15.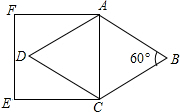 如图,在菱形ABCD中,∠B=60°,若正方形ACEF的周长为a,菱形ABCD的周长为b,则a与b的大小关系为( )
如图,在菱形ABCD中,∠B=60°,若正方形ACEF的周长为a,菱形ABCD的周长为b,则a与b的大小关系为( )
 如图,在菱形ABCD中,∠B=60°,若正方形ACEF的周长为a,菱形ABCD的周长为b,则a与b的大小关系为( )
如图,在菱形ABCD中,∠B=60°,若正方形ACEF的周长为a,菱形ABCD的周长为b,则a与b的大小关系为( )| A. | a>b | B. | a<b | C. | a=b | D. | 无法确定 |
12.抛物线y=$\frac{1}{2}$x2,y=-2x2,y=$\frac{2}{3}$x2共有的性质是( )
| A. | 开口向下 | B. | 对称轴是y轴 | ||
| C. | 都有最低点 | D. | y随x的增大而减小 |
 如图所示,将网络中△ABC绕点P逆时针旋转90°,得△A′B′C′,画出△A′B′C′.
如图所示,将网络中△ABC绕点P逆时针旋转90°,得△A′B′C′,画出△A′B′C′. 如图,在?ABCD中,AC=2,∠ADB=90°,∠BCD=45°,求BD的长.
如图,在?ABCD中,AC=2,∠ADB=90°,∠BCD=45°,求BD的长.