题目内容
9. 如图,在?ABCD中,AC=2,∠ADB=90°,∠BCD=45°,求BD的长.
如图,在?ABCD中,AC=2,∠ADB=90°,∠BCD=45°,求BD的长.
分析 由平行四边形的性质得出∠BAD=∠BCD=45°,OA=OC=$\frac{1}{2}$AC=1,OD=OB=$\frac{1}{2}$BD,得出△ABD是等腰直角三角形,得出AD=BD=2OD,设OD=x,则AD=BD=2x,由勾股定理得出方程,解方程求出x,即可得出BD的长.
解答 解:∵四边形ABCD是平行四边形,
∴∠BAD=∠BCD=45°,OA=OC=$\frac{1}{2}$AC=1,OD=OB=$\frac{1}{2}$BD,
∵∠ADB=90°,
∴△ABD是等腰直角三角形,
∴AD=BD=2OD,
设OD=x,则AD=BD=2x,
由勾股定理得:OD2+AD2=OA2,
即x2+(2x)2=12,
解得:x=±$\frac{\sqrt{5}}{5}$(负值舍去),
∴x=$\frac{\sqrt{5}}{5}$,
∴BD=$\frac{2\sqrt{5}}{5}$.
点评 本题考查了平行四边形的性质、等腰直角三角形的判定与性质、勾股定理;熟练掌握平行四边形的性质,并能进行推理论证与计算是解决问题的关键.

练习册系列答案
相关题目
17.若a<0,在1、a、1+a、1-a中最大的数是( )
| A. | 1 | B. | a | C. | 1+a | D. | 1-a |
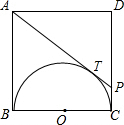 如图,在正方形ABCD中,以BC边为直径作半圆O,AP切半圆O于T点,交CD于P点,求AT:TP的值.
如图,在正方形ABCD中,以BC边为直径作半圆O,AP切半圆O于T点,交CD于P点,求AT:TP的值.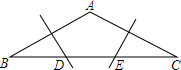 已知:如图,在△ABC中,AB=AC,∠A=120°,AB、AC的垂直平分线分交DE于点D、E.若BC=21cm,则DE=7cm.
已知:如图,在△ABC中,AB=AC,∠A=120°,AB、AC的垂直平分线分交DE于点D、E.若BC=21cm,则DE=7cm.