题目内容
17.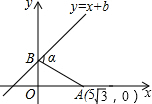 如图,已知点A(5$\sqrt{3}$,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=75°,则b=5.
如图,已知点A(5$\sqrt{3}$,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=75°,则b=5.
分析 首先根据直线y=x+b(b>0)与x轴、y轴分别交于点C、点B,求出点C,点B的坐标各是多少;然后根据∠α=75°,∠BCA=45°,应用三角形的外角的性质,求出∠BAC的度数是多少,进而求出b的值是多少即可.
解答 解:如图1,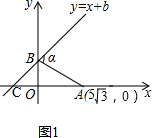 ,
,
∵直线y=x+b(b>0)与x轴、y轴分别交于点C、点B,
∴点C的坐标是(-b,0),点B的坐标是(0,b),
∵∠α=75°,∠BCA=45°,
∴∠BAC=75°-45°=30°,
∴$\frac{b}{5\sqrt{3}}=tan30°=\frac{\sqrt{3}}{3}$
解得b=5.
故答案为:5.
点评 (1)此题主要考查了解直角三角形问题,要熟练掌握,解答此题的关键是要明确解直角三角形要用到的关系:①锐角直角的关系:∠A+∠B=90°;②三边之间的关系:a2+b2=c2.
(2)此题还考查了一次函数图象上点的坐标特征,要熟练掌握,解答此题的关键是要明确:一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线.它与x轴的交点坐标是(-,0);与y轴的交点坐标是(0,b).直线上任意一点的坐标都满足函数关系式y=kx+b.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.下列四个数中,最大的数是( )
| A. | 3 | B. | -1 | C. | 0 | D. | $\sqrt{3}$ |
9.我市某水果生产基地,用30名工人进行采摘或加工水果,每名工人只能做其中一项工作.采摘的工人每人可以采摘水果400千克,加工罐头的工人每人可加工300千克.(加工水果数量不能多于采摘数量)设有x名工人进行水果采摘.
(1)①加工罐头的工人为(30-x)人,可以加工罐头300(30-x)千克;(用含x的式子表示)
②采摘水果的工人至少多少人?
(2)直接出售和加工罐头出售的利润如表:
要使直接出售所获利润不超过总利润的25%,请问应如何分配工人?所获最大利润是多少?
(1)①加工罐头的工人为(30-x)人,可以加工罐头300(30-x)千克;(用含x的式子表示)
②采摘水果的工人至少多少人?
(2)直接出售和加工罐头出售的利润如表:
| 销售方式 | 直接出售 | 加工成罐头销售 |
| 利润(元/千克) | 4 | 10 |
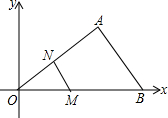 如图,在平面直角坐标系中,△AOB的三个顶点的坐标分别是A(4,3),O(0,0),B(6,0).点M是OB边一点,过点M作MN∥AB,若点M的坐标为(1,0)时,点N的坐标为($\frac{2}{3}$,$\frac{1}{2}$).
如图,在平面直角坐标系中,△AOB的三个顶点的坐标分别是A(4,3),O(0,0),B(6,0).点M是OB边一点,过点M作MN∥AB,若点M的坐标为(1,0)时,点N的坐标为($\frac{2}{3}$,$\frac{1}{2}$).
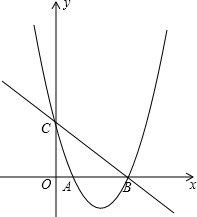 如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴相交于A,B两点,与y轴相交于点C,直线y=kx+n(k≠0)经过B,C两点,已知A(1,0),C(0,3),且BC=5.
如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴相交于A,B两点,与y轴相交于点C,直线y=kx+n(k≠0)经过B,C两点,已知A(1,0),C(0,3),且BC=5.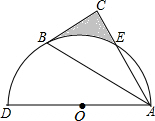 如图,以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点,交直角边AC于点E.点B、E恰好是半圆弧的三等分点.若AD=4,则图中阴影部分的面积为$\frac{3\sqrt{3}}{2}$-$\frac{2π}{3}$.
如图,以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点,交直角边AC于点E.点B、E恰好是半圆弧的三等分点.若AD=4,则图中阴影部分的面积为$\frac{3\sqrt{3}}{2}$-$\frac{2π}{3}$.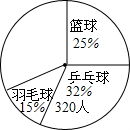 为了了解某校学生对篮球、足球、羽毛球、乒乓球、网球等五类的喜爱,小李采用了抽样调查,在绘制扇形图时,由于时间仓促,还有足球、网球等信息还没有绘制完成,如图所示,根据图中的信息,这批被抽样调查的学生最喜欢足球的人数不可能是( )
为了了解某校学生对篮球、足球、羽毛球、乒乓球、网球等五类的喜爱,小李采用了抽样调查,在绘制扇形图时,由于时间仓促,还有足球、网球等信息还没有绘制完成,如图所示,根据图中的信息,这批被抽样调查的学生最喜欢足球的人数不可能是( )