题目内容
5.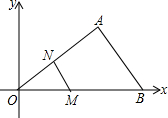 如图,在平面直角坐标系中,△AOB的三个顶点的坐标分别是A(4,3),O(0,0),B(6,0).点M是OB边一点,过点M作MN∥AB,若点M的坐标为(1,0)时,点N的坐标为($\frac{2}{3}$,$\frac{1}{2}$).
如图,在平面直角坐标系中,△AOB的三个顶点的坐标分别是A(4,3),O(0,0),B(6,0).点M是OB边一点,过点M作MN∥AB,若点M的坐标为(1,0)时,点N的坐标为($\frac{2}{3}$,$\frac{1}{2}$).
分析 过N,A分别作NE⊥x轴于E,AF⊥x轴于F,证明△ONM∽△OAB和△ONE∽△OAF,即可得到结论.
解答  解:过N,A分别作NE⊥x轴于E,AF⊥x轴于F,
解:过N,A分别作NE⊥x轴于E,AF⊥x轴于F,
∴NE∥AF,
∵A(4,3),B(6,0),M(1,0),
∴AF=3,OF=4,OB=6,OM=1,
∵MN∥AB,
∴△ONM∽△OAB,
∴$\frac{NE}{AF}=\frac{OM}{OB}$,
即$\frac{NE}{3}=\frac{1}{6}$,
∴NE=$\frac{1}{2}$
∵NE∥AF,
∴△ONE∽△OAF,
∴$\frac{OE}{OF}=\frac{NE}{AF}$,
即$\frac{OE}{4}=\frac{\frac{1}{2}}{3}$,
∴OE=$\frac{2}{3}$,
∴N($\frac{2}{3}$,$\frac{1}{2}$),
故答案为:($\frac{2}{3}$,$\frac{1}{2}$).
点评 本题考查了相似三角形的判定和性质,直角坐标系中点的坐标特征,正确的作出辅助线是解题的关键.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
16.下列运算正确的是( )
| A. | 2a2•3a3=6a6 | B. | 2xa+xa=3x2a2 | C. | (-2a)3=-6a3 | D. | a5÷a4=a |
13.在江岸区某初中,参加跳高的16名运动员的成绩如表:
那么这些运动员跳高成绩的众数是( )
| 成绩(m) | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
| 人数 | 2 | 2 | 4 | 3 | 3 | 2 |
| A. | 4 | B. | 1.75 | C. | 1.70 | D. | 1.65 |
10.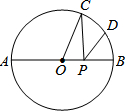 如图,已知⊙O的半径为R,C、D是直径AB的同侧圆周上的两点,弧AC的度数为100°弧BC=2弧BD,动点P在线段AB上,则PC+PD的最小值为( )
如图,已知⊙O的半径为R,C、D是直径AB的同侧圆周上的两点,弧AC的度数为100°弧BC=2弧BD,动点P在线段AB上,则PC+PD的最小值为( )
 如图,已知⊙O的半径为R,C、D是直径AB的同侧圆周上的两点,弧AC的度数为100°弧BC=2弧BD,动点P在线段AB上,则PC+PD的最小值为( )
如图,已知⊙O的半径为R,C、D是直径AB的同侧圆周上的两点,弧AC的度数为100°弧BC=2弧BD,动点P在线段AB上,则PC+PD的最小值为( )| A. | R | B. | $\sqrt{2}$R | C. | $\sqrt{3}$R | D. | $\frac{\sqrt{5}}{2}$R |

 4个大小相同的正方体积木摆放成如图所示的几何体,其主视图是( )
4个大小相同的正方体积木摆放成如图所示的几何体,其主视图是( )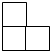
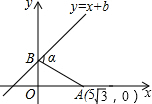 如图,已知点A(5$\sqrt{3}$,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=75°,则b=5.
如图,已知点A(5$\sqrt{3}$,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=75°,则b=5. 某海域有A,B两个港口,B港口在A港口北偏西30°方向上,距A港口60海里,有一艘船从A港口出发,沿东北方向行驶一段距离后,到达位于B港口南偏东75°方向的C处,求该船与B港口之间的距离即CB的长(结果保留根号).
某海域有A,B两个港口,B港口在A港口北偏西30°方向上,距A港口60海里,有一艘船从A港口出发,沿东北方向行驶一段距离后,到达位于B港口南偏东75°方向的C处,求该船与B港口之间的距离即CB的长(结果保留根号).