题目内容
8.先化简,再求值:$({x+1-\frac{3x}{{{x^2}-x}}})÷({\frac{x^2}{x-1}-4})$,其中x=2-$\sqrt{2}$.分析 先算括号内的减法,把除法变成乘法,算乘法,最后代入求出即可.
解答 解:$({x+1-\frac{3x}{{{x^2}-x}}})÷({\frac{x^2}{x-1}-4})$
=[$\frac{x+1}{1}$-$\frac{3x}{x(x-1)}$]÷[$\frac{{x}^{2}}{x-1}$-$\frac{4(x-1)}{x-1}$]
=$\frac{{x}^{2}-4}{x-1}$÷$\frac{{x}^{2}-4x+4}{x-1}$
=$\frac{(x+2)(x-2)}{x-1}$•$\frac{x-1}{(x-2)^{2}}$
=$\frac{x+2}{x-2}$,
当x=2-$\sqrt{2}$时,原式=$\frac{4-\sqrt{2}}{-\sqrt{2}}$=1-2$\sqrt{2}$.
点评 此题考查了分式的化简求值和二次根式的混合运算的应用,熟练掌握运算法则是解本题的关键,注意运算顺序.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
19.一元一次方程组$\left\{\begin{array}{l}{x+3y=2}\\{x-2y=7}\end{array}\right.$的解的情况是( )
| A. | $\left\{\begin{array}{l}{x=5}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=8}\\{y=-2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=9}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=3}\\{y=-2}\end{array}\right.$ |
16.下列运算正确的是( )
| A. | 2a2•3a3=6a6 | B. | 2xa+xa=3x2a2 | C. | (-2a)3=-6a3 | D. | a5÷a4=a |
13.在江岸区某初中,参加跳高的16名运动员的成绩如表:
那么这些运动员跳高成绩的众数是( )
| 成绩(m) | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
| 人数 | 2 | 2 | 4 | 3 | 3 | 2 |
| A. | 4 | B. | 1.75 | C. | 1.70 | D. | 1.65 |
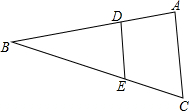 如图,在△ABC中,点D、点E分别在AB、BC边上,且DE∥AC,DE=2,AC=3,BE=4,则BC长度为6.
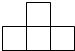
如图,在△ABC中,点D、点E分别在AB、BC边上,且DE∥AC,DE=2,AC=3,BE=4,则BC长度为6. 4个大小相同的正方体积木摆放成如图所示的几何体,其主视图是( )
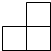
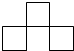
4个大小相同的正方体积木摆放成如图所示的几何体,其主视图是( )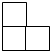
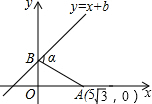 如图,已知点A(5$\sqrt{3}$,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=75°,则b=5.
如图,已知点A(5$\sqrt{3}$,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=75°,则b=5.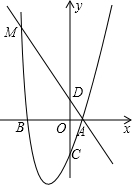 如图,二次函数y=x2+bx+c的图象经过A(1,0),B(-3,0)两点,与y轴交于点C,过点A的直线与y轴交干点D,与抛物线交于点M,且tan∠BAM=1.
如图,二次函数y=x2+bx+c的图象经过A(1,0),B(-3,0)两点,与y轴交于点C,过点A的直线与y轴交干点D,与抛物线交于点M,且tan∠BAM=1.