题目内容
10. 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于点A﹙-2,-5﹚C﹙5,n﹚,交y轴于点B,交x轴于点D.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于点A﹙-2,-5﹚C﹙5,n﹚,交y轴于点B,交x轴于点D.(1)求反比例函数y=$\frac{m}{x}$和一次函数y=kx+b的表达式;
(2)连接OA,OC.求△AOC的面积.
(3)直接写kx+b-$\frac{m}{x}$>0的解集.
分析 (1)利用待定系数法即可求得反比例函数和一次函数的解析式;
(2)首先求得B的坐标,然后根据S△AOC=S△AOB+S△BOC求解;
(3)kx+b-$\frac{m}{x}$>0的解集就是一次函数的图象在反比例函数的图象上边时对应的x的范围.
解答 解:(1)∵反比例函数y=$\frac{m}{x}$的图象经过点A﹙-2,-5﹚,
∴m=(-2)×(-5)=10.
∴反比例函数的表达式为y=$\frac{10}{x}$.
∵点C﹙5,n﹚在反比例函数的图象上,
∴n=$\frac{10}{5}$=2.
∴C的坐标为﹙5,2﹚.
∵一次函数的图象经过点A,C,将这两个点的坐标代入y=kx+b,得
$\left\{\begin{array}{l}{-5=-2k+b}\\{2=5k+b}\end{array}\right.$ 解得$\left\{\begin{array}{l}{k=1}\\{b=-3}\end{array}\right.$,
∴所求一次函数的表达式为y=x-3.
(2)∵一次函数y=x-3的图象交y轴于点B,
∴B点坐标为﹙0,-3﹚.
∴OB=3.
∵A点的横坐标为-2,C点的横坐标为5,…(7分)
∴S△AOC=S△AOB+S△BOC=$\frac{1}{2}$OB•|-2)+$\frac{1}{2}$OB×5=$\frac{1}{2}$OB(2+5)=$\frac{21}{2}$.
(3)x的范围是:-2<x<0或x>5.
点评 本题考查了反比例函数与一次函数的交点,当有两个函数的时候,着重使用一次函数,体现了方程思想,综合性较强.

练习册系列答案
相关题目
15.按下面的程序计算,若开始输入的x为正数,最后输出的结果为56,则满足条件的x的不同的值有( )个.


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20. 某学校举行一次数学知识竞赛,任选10名参赛学生的成绩并划分等级,制作成如下统计表和扇形统计图
某学校举行一次数学知识竞赛,任选10名参赛学生的成绩并划分等级,制作成如下统计表和扇形统计图
请回答下列问题:
(1)小华同学这次测试的成绩是87分,则他的成绩等级是A;
(2)求扇形统计图中C的圆心角的度数;
(3)该校将从这次竞赛的学生中,选拔成绩优异的学生参加复赛,并会对这批学生进行连续两个月的培训,每个月成绩提高的百分率均为10%,如果要求复赛的成绩不低于95分,那么学校应选取不低于多少分(取整数)的学生入围复赛?
 某学校举行一次数学知识竞赛,任选10名参赛学生的成绩并划分等级,制作成如下统计表和扇形统计图
某学校举行一次数学知识竞赛,任选10名参赛学生的成绩并划分等级,制作成如下统计表和扇形统计图 | 编号 | 成绩 | 等级 | 编号 | 成绩 | 等级 |
| ① | 90 | A | ⑥ | 76 | B |
| ② | 78 | B | ⑦ | 85 | A |
| ③ | 72 | C | ⑧ | 82 | B |
| ④ | 79 | B | ⑨ | 77 | B |
| ⑤ | 92 | A | ⑩ | 69 | C |
(1)小华同学这次测试的成绩是87分,则他的成绩等级是A;
(2)求扇形统计图中C的圆心角的度数;
(3)该校将从这次竞赛的学生中,选拔成绩优异的学生参加复赛,并会对这批学生进行连续两个月的培训,每个月成绩提高的百分率均为10%,如果要求复赛的成绩不低于95分,那么学校应选取不低于多少分(取整数)的学生入围复赛?
 如图,是由若干个相同的小正反体组成的几何体,如果从上面观察这个几何体得到的平面图形是( )
如图,是由若干个相同的小正反体组成的几何体,如果从上面观察这个几何体得到的平面图形是( )



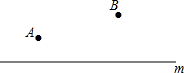 如图,某地由于居民增多,要在公路m上增加一个公共汽车站,A,B是路边两个新建小区,这个公共汽车站建在什么位置,能使两个小区到车站的路程一样长?(保留作图痕迹,不写作法)
如图,某地由于居民增多,要在公路m上增加一个公共汽车站,A,B是路边两个新建小区,这个公共汽车站建在什么位置,能使两个小区到车站的路程一样长?(保留作图痕迹,不写作法)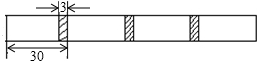 如图,将长为30cm、宽相等的长方形白纸,按如图所示的方法粘合起来,粘合部分的宽为3cm.则x张白纸粘合后的总长度为27x+3cm(用含x的代数式表示).
如图,将长为30cm、宽相等的长方形白纸,按如图所示的方法粘合起来,粘合部分的宽为3cm.则x张白纸粘合后的总长度为27x+3cm(用含x的代数式表示). 作图题
作图题