题目内容
 如图所示,过?ABCD的对角线的交点O任意画一条直线l,分别交AD、BC于点E、F,l将平行四边形分成两个四边形,这两个四边形是否关于点O成中心对称?请说明理由.
如图所示,过?ABCD的对角线的交点O任意画一条直线l,分别交AD、BC于点E、F,l将平行四边形分成两个四边形,这两个四边形是否关于点O成中心对称?请说明理由.考点:中心对称
专题:
分析:判断两个四边形是否关于点O中心对称可以转换为判断两个四边形的顶点是否关于点O对称即可.
解答:解:这两个四边形关于点O成中心对称.
∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,
∵EF、AC、BD都经过点O,
∴EO=FO,
∴点A与点C,点B与点D,点E与点F均关于点O成中心对称,
∴这两个四边形关于点O成中心对称.
∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,
∵EF、AC、BD都经过点O,
∴EO=FO,
∴点A与点C,点B与点D,点E与点F均关于点O成中心对称,
∴这两个四边形关于点O成中心对称.
点评:本题考查了中心对称的知识,解题的关键是判断对应的顶点关于O点中心对称,难度不大.

练习册系列答案
相关题目
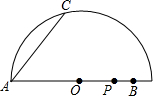 已知线段AB为半圆O的直径,AB=10cm,AC=6cm,点P为AB上一动点,P由B向A以2cm/s的速度运动,到达A点后停止运动.设P点的运动时间为t秒,当t为何值时,△ACP为等腰三角形?
已知线段AB为半圆O的直径,AB=10cm,AC=6cm,点P为AB上一动点,P由B向A以2cm/s的速度运动,到达A点后停止运动.设P点的运动时间为t秒,当t为何值时,△ACP为等腰三角形?