题目内容
20.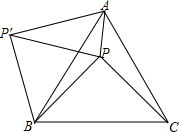 如图,P是正△ABC内一点,∠APC=130°,将△BPC绕点B逆时针方向旋转60°得到△BP′A,连接PP′,当∠BPC为多少度时,△APP′是等腰三角形?
如图,P是正△ABC内一点,∠APC=130°,将△BPC绕点B逆时针方向旋转60°得到△BP′A,连接PP′,当∠BPC为多少度时,△APP′是等腰三角形?
分析 根据旋转的性质得出△P′PB是等边三角形,得出∠P′PB=∠PP′B=60°,设∠BPC=x时,由△APP′是等腰三角形,则∠AP′B=x,∠AP′P=x-60°,分三种情况分别讨论求得∠APP′的值,根据∠APP′+∠P′PB+∠BPC+∠APC=360°,列出等式即可求得.
解答 解:∵PB=P′B,∠PBP′=60°,
∴△P′PB是等边三角形,
∴∠P′PB=∠PP′B=60°,
设∠BPC=x时,由△APP′是等腰三角形,则∠AP′B=x,
∴∠AP′P=x-60°,
①当P′A=P′P时,则∠P′PA=∠PAP′=$\frac{180°-(x-60°)}{2}$,
∵∠APP′+∠P′PB+∠BPC+∠APC=360°,
∴$\frac{180°-(x-60°)}{2}$+60°+x+130°=360°,
解得x=100°;
②当P′A=PA时,则∠P′PA=∠PP′A=x-60°
∵∠APP′+∠P′PB+∠BPC+∠APC=360°,
∴x-60°+60°+x+130°=360°,
解得x=115°;
③当P′P=PA时,则∠P′PA=180°-2(x-60°)=300°-2x
∵∠APP′+∠P′PB+∠BPC+∠APC=360°,
∴300°-2x+60°+x+130°=360°,
解得x=130°;
所以,当∠BPC为100°或115°或130°,△APP′是等腰三角形.
点评 本题考查了旋转的性质,等边三角形的判定和性质,等腰三角形的判定等,熟练掌握性质定理是解题的关键.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
9. 如图所示的空心几何体的俯视图是( )
如图所示的空心几何体的俯视图是( )
 如图所示的空心几何体的俯视图是( )
如图所示的空心几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
10.若(x-4)(x+n)=x2+mx-32,则m、n的值分别是( )
| A. | 4,8 | B. | 4,-8 | C. | -4,8 | D. | -4,-8 |
 如图,梯形ABCD中,AD∥BC,AC⊥BD,垂足为H,∠DBE=∠CBE,BD=BC,求证:FH•AC=FC2+FC•FH.
如图,梯形ABCD中,AD∥BC,AC⊥BD,垂足为H,∠DBE=∠CBE,BD=BC,求证:FH•AC=FC2+FC•FH.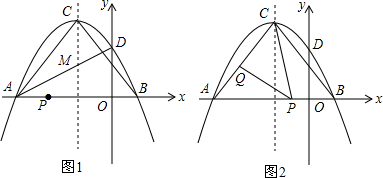
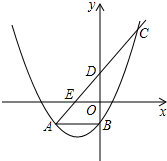 如图,抛物线y=ax2+2ax+c与直线y=x+b交于A(-2,-1)、C(1,2)两点,与y轴交于B,D、E是直线y=x+b与坐标轴的交点,
如图,抛物线y=ax2+2ax+c与直线y=x+b交于A(-2,-1)、C(1,2)两点,与y轴交于B,D、E是直线y=x+b与坐标轴的交点,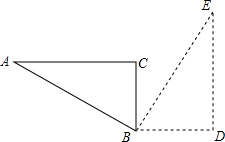 如图,Rt△ABC中,∠A=30°,AB=4cm,将△ABC绕顶点B按顺时针方向旋转90°到△BDE的位置,则:
如图,Rt△ABC中,∠A=30°,AB=4cm,将△ABC绕顶点B按顺时针方向旋转90°到△BDE的位置,则: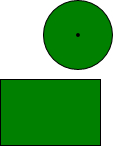 这是公园里两块形状不同的草坪,现在要修一条笔直的小路同时穿过这两块草坪,而且同时把两块草坪分成面积相同的两部分,如果你是设计师,你怎样设计这条小路?
这是公园里两块形状不同的草坪,现在要修一条笔直的小路同时穿过这两块草坪,而且同时把两块草坪分成面积相同的两部分,如果你是设计师,你怎样设计这条小路?