题目内容
5.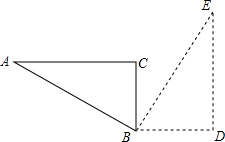 如图,Rt△ABC中,∠A=30°,AB=4cm,将△ABC绕顶点B按顺时针方向旋转90°到△BDE的位置,则:
如图,Rt△ABC中,∠A=30°,AB=4cm,将△ABC绕顶点B按顺时针方向旋转90°到△BDE的位置,则:(1)点A运动的路径长为2πcm;
(2)点C运动的路径长为πcm;
(3)线段BC扫过的面积为πcm2;
(4)线段AB扫过的面积为4πcm2;
(5)线段AC扫过的面积为3πcm2;
(6)△ABC扫过的面积为(4π+2$\sqrt{3}$)cm2.
分析 (1)根据弧长公式求出$\widehat{AE}$即可;
(2)先根据直角三角形30°角所对的直角边等于斜边的一半得出BC=$\frac{1}{2}$AB=2cm,再根据弧长公式求出$\widehat{CD}$即可;
(3)线段BC扫过的面积是以BC为半径的圆面积的$\frac{1}{4}$;
(4)线段AB扫过的面积是以AB为半径的圆面积的$\frac{1}{4}$;
(5)线段AC扫过的面积=AB扫过的扇形面积-BC扫过的扇形面积;
(6)△ABC扫过的面积=线段AB扫过的面积+三角形ABC的面积.
解答  解:(1)点A运动的路径长为:$\frac{90π×4}{180}$=2π(cm);
解:(1)点A运动的路径长为:$\frac{90π×4}{180}$=2π(cm);
(2)∵Rt△ABC中,∠A=30°,AB=4cm,
∴BC=$\frac{1}{2}$AB=2cm,
∴点C运动的路径长为:$\frac{90π×2}{180}$=π(cm);
(3)线段BC扫过的面积为:$\frac{1}{4}$π×22=π(cm2);
(4)线段AB扫过的面积为:$\frac{1}{4}$π×42=4π(cm2);
(5)线段AC扫过的面积为:4π-π=3π(cm2);
(6)∵Rt△ABC中,∠A=30°,AB=4cm,
∴AC=AB•cosA=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$(cm),
∴△ABC扫过的面积为:4π+$\frac{1}{2}$×2×2$\sqrt{3}$=4π+2$\sqrt{3}$(cm2).
故答案为2πcm,πcm,πcm2,4πcm2,3πcm2,(4π+2$\sqrt{3}$)cm2.
点评 本题考查了旋转的性质,直角三角形的性质,弧长的计算,扇形的面积的计算,熟记性质与计算公式是解题的关键.

练习册系列答案
相关题目
 如图,已知△ABC中,CD是∠ACB的角平分线,EF垂直平分CD交AB延长线于点F,求证:DF2=AF•BF.
如图,已知△ABC中,CD是∠ACB的角平分线,EF垂直平分CD交AB延长线于点F,求证:DF2=AF•BF.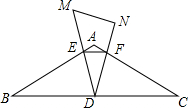 已知△ABC中,AB=AC=8,∠B=30°,D为BC上中点,Rt△DNM中,∠MDN=30°,D为定点,DM、DN交AB、AC于E、F.
已知△ABC中,AB=AC=8,∠B=30°,D为BC上中点,Rt△DNM中,∠MDN=30°,D为定点,DM、DN交AB、AC于E、F.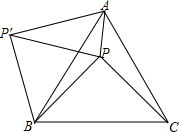 如图,P是正△ABC内一点,∠APC=130°,将△BPC绕点B逆时针方向旋转60°得到△BP′A,连接PP′,当∠BPC为多少度时,△APP′是等腰三角形?
如图,P是正△ABC内一点,∠APC=130°,将△BPC绕点B逆时针方向旋转60°得到△BP′A,连接PP′,当∠BPC为多少度时,△APP′是等腰三角形?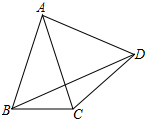 如图,△ABC中,AB=AC,∠BAC=40°,边AB绕点A逆时针旋转m°,(0<m<360)得到线段AD,连接BD、DC.若△BDC为等腰三角形,则m所有可能的取值是20°,80°,200°,320°.
如图,△ABC中,AB=AC,∠BAC=40°,边AB绕点A逆时针旋转m°,(0<m<360)得到线段AD,连接BD、DC.若△BDC为等腰三角形,则m所有可能的取值是20°,80°,200°,320°.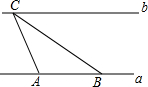 如图,直线a∥b,定点A、B在直线a上,动点C在直线b上从左向右运动,在此运动过程中:
如图,直线a∥b,定点A、B在直线a上,动点C在直线b上从左向右运动,在此运动过程中: