题目内容
5.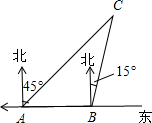 如图,有A、B两艘船在大海中航行,B船在A船的正东方向,且两船保持20海里的距离,某一时刻这两艘船同时测得在A的东北方向,B的北偏东15°方向有另一艘船C,那么此时船C与船B的距离是20$\sqrt{2}$海里(结果保留根号).
如图,有A、B两艘船在大海中航行,B船在A船的正东方向,且两船保持20海里的距离,某一时刻这两艘船同时测得在A的东北方向,B的北偏东15°方向有另一艘船C,那么此时船C与船B的距离是20$\sqrt{2}$海里(结果保留根号).
分析 首先过点B作BD⊥AC于点D,进而利用BD=AB•sin∠BAD,BC=$\frac{BD}{sin∠BCD}$求出即可.
解答  解:过点B作BD⊥AC于点D,
解:过点B作BD⊥AC于点D,
由题意可知:∠BAC=45°,∠ABC=90°+15°=105°,
则∠ACB=180°-∠BAC-∠ABC=30°,
在Rt△ABD中,BD=AB•sin∠BAD=20×$\frac{\sqrt{2}}{2}$=10$\sqrt{2}$,
在Rt△BCD中,BC=$\frac{BD}{sin∠BCD}$=20$\sqrt{2}$.
答:此时船C与船B的距离是20$\sqrt{2}$海里.
故答案为20$\sqrt{2}$.
点评 此题考查了解直角三角形的应用-方向角问题.此题难度适中,注意能借助于方向角构造直角三角形,并利用解直角三角形的知识求解是解此题的关键.

练习册系列答案
相关题目
15.对甲、乙两户家庭全年各项支出的统计如图所示,已知甲户居民的衣着支出与乙户相同,下面根据统计,对两户家庭教育支出的费用做出判断,正确的是( )
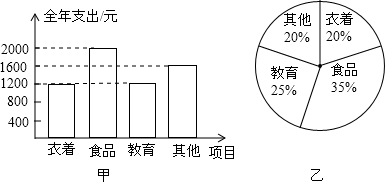

| A. | 甲比乙大 | B. | 乙比甲大 | C. | 甲、乙一样大 | D. | 无法确定 |
16.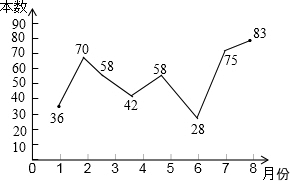 小明根据去年1~8月本班同学参加学校组织的“书香校园”活动中全班同学的课外阅读书籍的数量(单位:本),绘制了如图所示折线统计图,下列说法正确的是( )
小明根据去年1~8月本班同学参加学校组织的“书香校园”活动中全班同学的课外阅读书籍的数量(单位:本),绘制了如图所示折线统计图,下列说法正确的是( )
 小明根据去年1~8月本班同学参加学校组织的“书香校园”活动中全班同学的课外阅读书籍的数量(单位:本),绘制了如图所示折线统计图,下列说法正确的是( )
小明根据去年1~8月本班同学参加学校组织的“书香校园”活动中全班同学的课外阅读书籍的数量(单位:本),绘制了如图所示折线统计图,下列说法正确的是( )| A. | 阅读数量的平均数是57 | B. | 阅读数量的众数是42 | ||
| C. | 阅读数量的中位数是58 | D. | 有4个月的阅读数量超过60本 |
14.给出四个数0,-$\sqrt{2}$,-$\frac{11}{7}$,$\sqrt{4}$,其中为无理数的是( )
| A. | 0 | B. | -$\frac{11}{7}$ | C. | -$\sqrt{2}$ | D. | $\sqrt{4}$ |
15.一元二次方程x2-3x-5=0的根的情况是( )
| A. | 有两个相等的实数根 | B. | 没有实数根 | ||
| C. | 无法确定是否有实数根 | D. | 有两个不相等的实数根 |
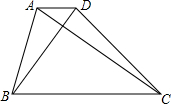 如图,梯形ABCD中,AD∥BC,AD=2,BC=8,AC=8,BD=6,则梯形ABCD的高为4.8.
如图,梯形ABCD中,AD∥BC,AD=2,BC=8,AC=8,BD=6,则梯形ABCD的高为4.8.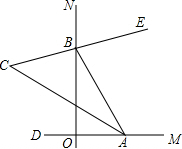 如图,∠MON=90°,点A,B分别在射线OM、ON上移动,BE是∠ABN的平分线,BE的反向延长线与∠OAB平分线相交于点C,试问:∠ACB的大小是否发生变化?如果保持不变,请给出证明;如果随点A、B移动发生变化,请求出变化范围.
如图,∠MON=90°,点A,B分别在射线OM、ON上移动,BE是∠ABN的平分线,BE的反向延长线与∠OAB平分线相交于点C,试问:∠ACB的大小是否发生变化?如果保持不变,请给出证明;如果随点A、B移动发生变化,请求出变化范围.