题目内容
7.某中学在实施快乐大课间之前组织过“我最喜欢的球类”的调查活动,每个学生仅选择一项,通过对学生的随机抽样调查得到一组数据,如图是根据这组数据绘制成的不完整统计图.(1)求出被调查的学生人数;
(2)把折线统计图补充完整;
(3)小亮、小莹、小芳和大刚到学校乒乓球室打乒乓球,当时只有一副空球桌,他们只能选两人打第一场.如果确定小亮打第一场,其余三人用“手心、手背”的方法确定谁获胜谁打第一场若三人中有一人出的与其余两人不同则获胜;若三人出的都相同则平局.已知大刚出手心,请用树状图分析大刚获胜的概率是多少?

分析 (1)根据乒乓球人数和所占的百分比即可求出总人数;
(2)用总人数乘以足球所占的百分比求出足球的人数,再用总人数减去篮球、足球、乒乓球和其他的人数,求出羽毛球的人数,从而补全折线统计图;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与大刚获胜的情况数,再利用概率公式即可求得答案.
解答  解:(1)被调查的学生数为:40÷20%=200(人);
解:(1)被调查的学生数为:40÷20%=200(人);
(2)医生的人数是:200×15%=30(人);
教师的人数是:200-30-40-20-70=40(人),
补图如下:
(3)如图:
由树状图可知:三人伸手的情况有(手心、手心、手心),(手心,手心,手背),(手心,手背,手心),(手心,手背,手背)4种,每种情况出现的可能性都是相同的,其中大刚伸手心与其他两人不同的情况有1种,所以P大刚=$\frac{1}{4}$,
所以大刚获胜的概率为$\frac{1}{4}$.
点评 此题考查了树状图法与列表法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
17.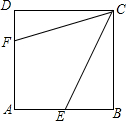 如图,正方形ABCD的边长为6,点E、F分别在AB,AD上,若点E为AB的中点,且满足BE+DF=EF,则EF的长为( )
如图,正方形ABCD的边长为6,点E、F分别在AB,AD上,若点E为AB的中点,且满足BE+DF=EF,则EF的长为( )
 如图,正方形ABCD的边长为6,点E、F分别在AB,AD上,若点E为AB的中点,且满足BE+DF=EF,则EF的长为( )
如图,正方形ABCD的边长为6,点E、F分别在AB,AD上,若点E为AB的中点,且满足BE+DF=EF,则EF的长为( )| A. | 4 | B. | 3$\sqrt{2}$ | C. | 5 | D. | 4$\sqrt{2}$ |
18. 如图,点P是直线y=$\frac{1}{2}$x+1上动点,点Q(0,m)是y轴负半轴上定点,连接PQ,当PQ的长度最小时,∠PQO的正弦值为( )
如图,点P是直线y=$\frac{1}{2}$x+1上动点,点Q(0,m)是y轴负半轴上定点,连接PQ,当PQ的长度最小时,∠PQO的正弦值为( )
 如图,点P是直线y=$\frac{1}{2}$x+1上动点,点Q(0,m)是y轴负半轴上定点,连接PQ,当PQ的长度最小时,∠PQO的正弦值为( )
如图,点P是直线y=$\frac{1}{2}$x+1上动点,点Q(0,m)是y轴负半轴上定点,连接PQ,当PQ的长度最小时,∠PQO的正弦值为( )| A. | $\frac{{2\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{1}{2}$ | D. | 和m的取值有关 |
2.下列运算结果正确的是( )
| A. | x2+x3=x5 | B. | x3•(3x)2=9x5 | C. | x5÷x=x5 | D. | x3•x2=x6 |
12.已知m、n是方程x2+1999x+7=0的两个根,则(m2+1998m+6)(n2+2000n+8)=( )
| A. | 1993 | B. | 1991 | C. | -1991 | D. | -1993 |
19.已知整式x2-2x的值为-1,则x2-2x+3的值为( )
| A. | -2 | B. | 2 | C. | -4 | D. | 4 |
 如图,在平面直角坐标系中,点A、C分别是一次函数y=-$\frac{3}{4}$x+3的图象与y轴、x轴的交点,抛物线y=$\frac{1}{4}$x2+bx+c经过B(-2,0)、D(6,3)两点.
如图,在平面直角坐标系中,点A、C分别是一次函数y=-$\frac{3}{4}$x+3的图象与y轴、x轴的交点,抛物线y=$\frac{1}{4}$x2+bx+c经过B(-2,0)、D(6,3)两点.