题目内容
6.在△ABC中,AB,BC,AC三边的长分别$\sqrt{2}$,$\sqrt{13}$,$\sqrt{17}$,求这个三角形的面积.
小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
(1)请你将△ABC的面积直接填写在横线上.2.5
思维拓展
(2)我们把上述求△ABC面积的方法叫做构图法.若△ABC三边的长分别为2$\sqrt{2}$a,$\sqrt{10}$a,$\sqrt{26}$a(a>0),请利用图2的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.
(3)若△ABC三边的长分别为$\sqrt{{m}^{2}+4{n}^{2}}$,$\sqrt{{m}^{2}+16{n}^{2}}$,2$\sqrt{{m}^{2}+{n}^{2}}$(m>0,n>0,m≠n),请运用构图法在图3指定区域内画出示意图,并求出△ABC的面积.
分析 (1)用长为4,宽为2的矩形减去3个三角形的面积,即可求得答案;
(2)2$\sqrt{2}$a是以2a,2a为直角边的直角三角形的斜边长;$\sqrt{10}$a是以a,3a为直角边的直角三角形的斜边长;$\sqrt{26}$a是以a,5a为直角边的直角三角形的斜边长;继而可作出三角形,然后求得面积;
(3)$\sqrt{{m}^{2}+4{n}^{2}}$是以m,2n为直角边的直角三角形的斜边长;$\sqrt{{m}^{2}+16{n}^{2}}$是以m,4n为直角边的直角三角形的斜边长;2$\sqrt{{m}^{2}+{n}^{2}}$是以2m,2n为直角边的直角三角形的斜边长;继而可作出三角形,然后求得三角形的面积.
解答 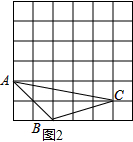 解:(1)S△ABC=2×4-$\frac{1}{2}$×1×1-$\frac{1}{2}$×3×2-$\frac{1}{2}$×1×4=2.5;
解:(1)S△ABC=2×4-$\frac{1}{2}$×1×1-$\frac{1}{2}$×3×2-$\frac{1}{2}$×1×4=2.5;
故答案为:2.5;
(2)如图2,AB=2$\sqrt{2}$a,BC=$\sqrt{10}$a,AC=$\sqrt{26}$a,
∴S△ABC=2a×5a-$\frac{1}{2}$×2a×2a-$\frac{1}{2}$×3a×a-$\frac{1}{2}$×a×5a=4a2;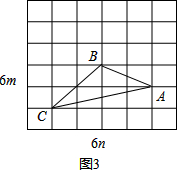 (3)如图3,AB=$\sqrt{{m}^{2}+4{n}^{2}}$,AC=$\sqrt{{m}^{2}+16{n}^{2}}$,BC=2$\sqrt{{m}^{2}+{n}^{2}}$;
(3)如图3,AB=$\sqrt{{m}^{2}+4{n}^{2}}$,AC=$\sqrt{{m}^{2}+16{n}^{2}}$,BC=2$\sqrt{{m}^{2}+{n}^{2}}$;
∴S△ABC=2m×4n-$\frac{1}{2}$×2m×2n-$\frac{1}{2}$×m×4n-$\frac{1}{2}$×m×2n=3mn.
点评 此题考查了勾股定理的应用以及三角形面积问题.注意掌握利用勾股定理的知识画无理数是解此题的关键.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 下面的长方体是由A,B,C,D四个选项中所示的四个几何体拼接而成的,而且这四个几何体都是由4个同样大小的正方体组成的,那么长方体中,第四部分所对应的几何体应是( )
下面的长方体是由A,B,C,D四个选项中所示的四个几何体拼接而成的,而且这四个几何体都是由4个同样大小的正方体组成的,那么长方体中,第四部分所对应的几何体应是( )



 青岛国际帆船中心要修建一处公共服务设施,使它到三所运动员公寓A、B、C的距离相等.(不写作法,但要保留作图痕迹)
青岛国际帆船中心要修建一处公共服务设施,使它到三所运动员公寓A、B、C的距离相等.(不写作法,但要保留作图痕迹) 已知如图,AD∥CF∥EB,AB=3,AC=5,DF=9,DA=2,CF=8,则,DE=$\frac{27}{5}$,EF=$\frac{18}{5}$,BE=4.
已知如图,AD∥CF∥EB,AB=3,AC=5,DF=9,DA=2,CF=8,则,DE=$\frac{27}{5}$,EF=$\frac{18}{5}$,BE=4.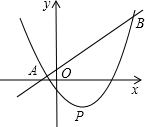 如图,直线y=kx+2k-1与抛物线y=kx2-2kx-4(k>0)相交于A,B两点,抛物线的顶点为P.
如图,直线y=kx+2k-1与抛物线y=kx2-2kx-4(k>0)相交于A,B两点,抛物线的顶点为P. 如图,C、D是以AB为直径的半圆上两点,且$\widehat{AD}$=$\widehat{CD}$
如图,C、D是以AB为直径的半圆上两点,且$\widehat{AD}$=$\widehat{CD}$