题目内容
15. 如图,AB为⊙O的直径,CD与⊙O相切于点D,CD⊥AC于C,AC交⊙O于E,CD=2CE.
如图,AB为⊙O的直径,CD与⊙O相切于点D,CD⊥AC于C,AC交⊙O于E,CD=2CE.(1)求证:AE=3CE;
(2)求$\frac{BC}{AD}$的值.
分析 (1)作辅助线,设CE=x,则CD=2x,证明△ECD∽△DCA,列比例式可得结论;
(2)证明四边形CEFD是矩形,则EF=CD=2x,CD∥BE,利用勾股定理分别表示BC和AD的长,相比即可.
解答  证明:(1)连接DE、OD、BE,交OD于F,
证明:(1)连接DE、OD、BE,交OD于F,
设CE=x,则CD=2x,
∵CD与⊙O相切于点D,
∴∠CDE=∠CAD,
∵∠ACD=∠ACD,
∴△ECD∽△DCA,
∴$\frac{EC}{DC}=\frac{CD}{AC}$,
∴AC=$\frac{C{D}^{2}}{EC}$=$\frac{4{x}^{2}}{x}$=4x,
∴AC=4CE,
∴AE=3CE;
(2)∵CD与⊙O相切于点D,
∴CD⊥OD,
∴∠CDO=90°,
∵AB是⊙O的直径,
∴∠AEB=90°,
∴∠CEB=90°,
∵CD⊥AC,
∴∠ACD=90°,
∴∠ACD=∠CEB=∠CDO=90°,
∴四边形CEFD是矩形,
∴EF=CD=2x,CD∥BE,
∴OD⊥BE,
∴BE=2EF=4x,
Rt△CEB中,BC2=CE2+BE2=x2+(4x)2=17x2,
BC=$\sqrt{17}$x,
Rt△ACD中,AD2=CD2+AC2=(2x)2+(4x)2=20x2,
AD=2$\sqrt{5}$x,
∴$\frac{BC}{AD}$=$\frac{\sqrt{17}x}{2\sqrt{5}x}$=$\frac{\sqrt{85}}{10}$.
点评 本题考查了相似三角形的性质和判定、矩形的性质和判定、圆的切线的性质、垂径定理、勾股定理,第一问题证明△ECD∽△DCA是关键,第二问证明四边形CEFD是矩形是关键,设未知数表示线段的长,根据未知数的关系确定线段的关系.

练习册系列答案
相关题目
3.二次函数y=ax2+bx+c(a,b,c为常数且a≠0)中的x与y的部分对应值如表:
已知表中有且只有一组数据错误,则这组错误数据中的x值是2.
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 0 | -3 | -4 | 1 | 0 | … |
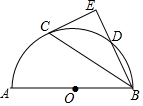 如图,点D是以AB为直径的半圆O上一点,连接BD,点C是$\widehat{AD}$的中点,过点C作直线BD的垂线,垂足为点E.
如图,点D是以AB为直径的半圆O上一点,连接BD,点C是$\widehat{AD}$的中点,过点C作直线BD的垂线,垂足为点E.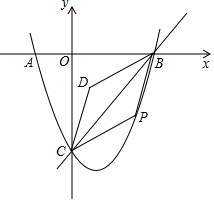 如图,在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于点A(-1,0),B(3,0),与y轴交于点C,作直线BC,点P是抛物线上一个动点(点P不与点B,C重合),连结PB,PC,以PB,PC为边作?CPBD,设?CPBD的面积为S,点P的横坐标为m.
如图,在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于点A(-1,0),B(3,0),与y轴交于点C,作直线BC,点P是抛物线上一个动点(点P不与点B,C重合),连结PB,PC,以PB,PC为边作?CPBD,设?CPBD的面积为S,点P的横坐标为m.