题目内容
11.有一副直角三角板,在三角板ABC中,∠BCA=90°,BC=4cm,AC=4$\sqrt{3}$cm.在三角板DEF中,∠FDE=90°,DF=DE=4cm.将这副直角三角板按如图(1)所示位置摆放,点C与点D重合,直角边BC与DE在同一条直线上.现固定三角板DEF,将三角板ABC沿射线DE方向以1cm/秒的速度平行移动,当点B运动到点E时停止运动.设运动的时间为t秒.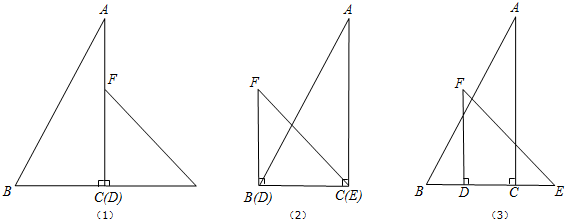
(1)如图(2),当三角板ABC运动到点C与点E重合时,设EF与BA交于点M,则$\frac{FM}{ME}$=$\frac{\sqrt{3}}{3}$;
(2)如图(3),在三角板ABC运动过程中,当t为何值时,AB经过点F;
(3)在三角板ABC运动过程中,设两块三角板重叠部分的面积为y,且0≤t≤4,求y与t的函数解析式,并求出对应的t的取值范围.
分析 (1)根据平行线分线段成比例定理,列出比例式即可解决问题.
(2)由DF∥AC,得$\frac{DF}{AC}$=$\frac{BD}{BC}$,求出BD,再求出CD即可解决问题.
(3)分两种情形:①当0≤t≤4-$\frac{4\sqrt{3}}{3}$,如图(4)中,重叠部分是梯形CDFM,②当4-$\frac{4\sqrt{3}}{3}$<t≤4时,重叠部分是五边形DCMGH,分别计算即可.
解答 解:(1)如图(2)中,
∵AC∥DF,
∴$\frac{FM}{ME}$=$\frac{DF}{AC}$=$\frac{4}{4\sqrt{3}}$=$\frac{\sqrt{3}}{3}$.
故答案为$\frac{\sqrt{3}}{3}$.
(2)如图(3)中,
∵DF∥AC,
∴$\frac{DF}{AC}$=$\frac{BD}{BC}$,
∴$\frac{4}{4\sqrt{3}}$=$\frac{BD}{4}$,
∴BD=$\frac{4\sqrt{3}}{3}$,
∴CD=BC-BD=4-$\frac{4\sqrt{3}}{3}$,
∴t=(4-$\frac{4\sqrt{3}}{3}$)÷1=4-$\frac{4\sqrt{3}}{3}$.
(3)①当0≤t≤4-$\frac{4\sqrt{3}}{3}$,如图(4)中,重叠部分是梯形CDFM.
y=$\frac{1}{2}$(DF+CM)•CD=$\frac{1}{2}$(4+4-t)•t═-$\frac{1}{2}$t2+8.
②当4-$\frac{4\sqrt{3}}{3}$<t≤4时,重叠部分是五边形DCMGH,
作DN⊥AC于N,设GN=NM=x,则AN=$\sqrt{3}$x,
由题意x+$\sqrt{3}$x=4$\sqrt{3}$-(4-t),
解得x=$\frac{4\sqrt{3}-(4-t)}{\sqrt{3}+1}$,
y=S△ABC-S△BDH-S△AGM=8$\sqrt{3}$-$\frac{1}{2}$(4-t)•$\sqrt{3}$(4-t)-$\frac{1}{2}$•[4$\sqrt{3}$-(4-t)]•$\frac{4\sqrt{3}-(4-t)}{\sqrt{3}+1}$=-$\frac{1-3\sqrt{3}}{4}$(4-t)2+(6-2$\sqrt{3}$)(4-t)+12-4$\sqrt{3}$.
综上所述y=$\left\{\begin{array}{l}{-\frac{1}{2}{t}^{2}+8}&{(0≤t≤4-\frac{4\sqrt{3}}{3})}\\{\frac{1-3\sqrt{3}}{4}(4-t)^{2}+(6-2\sqrt{3})(4-t)+12-4\sqrt{3}}&{(4-\frac{4\sqrt{3}}{3}<t≤4)}\end{array}\right.$.
点评 本题考查相似三角形的性质、平行线分线段成比例定理、特殊三角形的性质等知识,解题的关键是灵活灵活应用这些知识解决问题,学会分类讨论,学会利用分割法求多边形面积,属于中考压轴题.

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案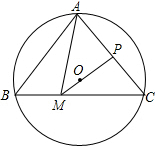 如图,△ABC内接于⊙O,若∠BAC=80°,∠C=50°,取AC中点P,连接PO并延长交BC于点M,连接AM,则∠BAM=( )
如图,△ABC内接于⊙O,若∠BAC=80°,∠C=50°,取AC中点P,连接PO并延长交BC于点M,连接AM,则∠BAM=( )| A. | 45° | B. | 30° | C. | 50° | D. | 55° |
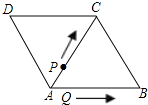 如图,△ABC和△ACD都是边长为2厘米的等边三角形,两个动点P,Q同时从A点出发,点P以0.5厘米/秒的速度沿A→C→B的方向运动,点Q以1厘米/秒的速度沿A→B→C→D的方向运动,当点Q运动到D点时,P、Q两点同时停止运动.设P、Q运动的时间为t秒
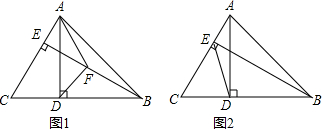
如图,△ABC和△ACD都是边长为2厘米的等边三角形,两个动点P,Q同时从A点出发,点P以0.5厘米/秒的速度沿A→C→B的方向运动,点Q以1厘米/秒的速度沿A→B→C→D的方向运动,当点Q运动到D点时,P、Q两点同时停止运动.设P、Q运动的时间为t秒 如图,在边长为1个单位长度的小正方形组成的网格中,A、B、C都是格点.
如图,在边长为1个单位长度的小正方形组成的网格中,A、B、C都是格点.