题目内容
5.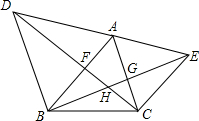 如图,△ABC中,∠A=60°,分别以AB、AC为边作等边△ABD、等边△ACE,连CD交AB于F,连BE交AC于G,CD、BE交于H点,在不添加辅助线的情况下,从图形中找出三组全等三角形,并选其中的两组进行证明.
如图,△ABC中,∠A=60°,分别以AB、AC为边作等边△ABD、等边△ACE,连CD交AB于F,连BE交AC于G,CD、BE交于H点,在不添加辅助线的情况下,从图形中找出三组全等三角形,并选其中的两组进行证明.
分析 由等边三角形的性质得出AD=AB,AE=AC,∠DAB=∠EAC=∠AEC=∠ACE=60°,由SAS证明△ACD≌△AEB,得出对应角相等∠ADF=∠ABG,再由ASA证明△ADF≌△ABG即可.
解答 解:△ACD≌△AEB,△ADF≌△ABG,△ACF≌△AEG;
∵△ABD和△ACE都为等边三角形,
∴AD=AB,AE=AC,∠DAB=∠EAC=∠AEC=∠ACE=60°,
∴∠DAB+∠BAC=∠EAC+∠BAC,
即∠DAC=∠BAE,
在△ACD和△AEB中,
$\left\{\begin{array}{l}{AD=AB}&{\;}\\{∠DAC=∠BAE}&{\;}\\{AC=AE}&{\;}\end{array}\right.$,
∴△ACD≌△AEB;
∴∠ADF=∠ABG,
在△ADF和△ABE中,
$\left\{\begin{array}{l}{∠DAF=∠BAG}&{\;}\\{AD=AB}&{\;}\\{∠ADF=∠ABG}&{\;}\end{array}\right.$,
∴△ADF≌△ABG(ASA).
点评 本题考查了等边三角形的性质、全等三角形的判定方法;熟练掌握等边三角形的性质,由等边三角形的性质得出相等的边好角是证明三角形全等的关键.

练习册系列答案
相关题目
20.若以三个数为三角形三边的长能构成直角三角形,我们就把它们称为一组勾股数,如3,4,5,勾股数之间存在一种奇妙的联系,观察下表,结合表中数的规律及相关知识,求出b,c的值
| 举例 | 猜 想 |
| 5、12、13 | 52=12+13 |
| 7、24、25 | 72=24+25 |
| … | … |
| 13、b、c | 132=b+c |
14.随着n的值变大,代数式$1+\frac{1}{n}$的值变的越来越接近于( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
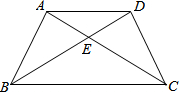 如图,在四边形ABCD中,AB=AD,AC与BD交于点E,∠ADB=∠ACB.
如图,在四边形ABCD中,AB=AD,AC与BD交于点E,∠ADB=∠ACB. 如图,△ABC中,AB=10,BC=8,AC=6,将△ABC折叠,使一边的两个端点重合,折痕为MN,求没有重合部分所成的三角形的周长.
如图,△ABC中,AB=10,BC=8,AC=6,将△ABC折叠,使一边的两个端点重合,折痕为MN,求没有重合部分所成的三角形的周长. 在等边三角形ABC,DE∥AB,DE与边AB、AC分别交于D、E,△ADE是等边三角形吗?试说明理由.
在等边三角形ABC,DE∥AB,DE与边AB、AC分别交于D、E,△ADE是等边三角形吗?试说明理由.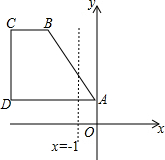 如图,已知四个点A(0,1),B(-3,4),C(-5,4),D(-5,1).
如图,已知四个点A(0,1),B(-3,4),C(-5,4),D(-5,1).