题目内容
4.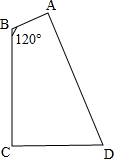 已知如图,四边形ABCD中,BC⊥CD,BA⊥AD,BA=2,AD=20,∠ABC=120°,求BC的长.
已知如图,四边形ABCD中,BC⊥CD,BA⊥AD,BA=2,AD=20,∠ABC=120°,求BC的长.
分析 作DA和CB的延长线交于E,先由∠ABC=120°得到∠ABE=60°,则∠E=30°,在△ABE中,根据含30度的直角三角形得到EB=2AB=4,AE=$\sqrt{3}$AB=2$\sqrt{3}$,则ED=EA+AD=20+2$\sqrt{3}$,再在Rt△ECD中计算出CE=$\frac{\sqrt{3}}{2}$ED=10$\sqrt{3}$+3,然后根据线段的和差关系即可求得BC的长.
解答 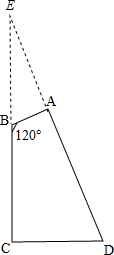 解:作DA和CB的延长线交于E,
解:作DA和CB的延长线交于E,
∵∠ABC=120°
∴∠ABE=60°,
∵BA⊥AD,
∴∠BAE=90°,
∴∠E=30°,
在Rt△ABE中,EB=2AB=4,AE=$\sqrt{3}$AB=2$\sqrt{3}$,
∴ED=EA+AD=20+2$\sqrt{3}$,
∵BC⊥CD,
∴∠C=90°,
在Rt△ECD中,CE=$\frac{\sqrt{3}}{2}$ED=10$\sqrt{3}$+3,
∴BC=CE-BE=10$\sqrt{3}$-1.
点评 此题考查了勾股定理,以及含30°直角三角形的性质,熟练掌握勾股定理和添加辅助线构成直角三角形是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.随着n的值变大,代数式$1+\frac{1}{n}$的值变的越来越接近于( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
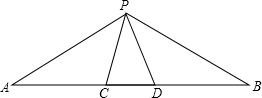 如图,点C,D在线段AB上,P是直线AB外一点,连接PA,PB,PC,PD.已知△PCD是等边三角形,如果CD2=AC•DB,求∠APB的度数.
如图,点C,D在线段AB上,P是直线AB外一点,连接PA,PB,PC,PD.已知△PCD是等边三角形,如果CD2=AC•DB,求∠APB的度数.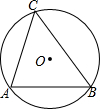 已知:如图,在△ABC中,AB=10,∠C=60°,求△ABC外接圆⊙O的半径r.
已知:如图,在△ABC中,AB=10,∠C=60°,求△ABC外接圆⊙O的半径r. 对于边长为4的等边三角形ABC,建立适当的平面直角坐标系,写出各个顶点的坐标.
对于边长为4的等边三角形ABC,建立适当的平面直角坐标系,写出各个顶点的坐标.