题目内容
完成下列有关函数的问题:
(1)函数y=-x上的点的坐标和为 ;
(2)函数y=x+1与x轴所夹的锐角为 ;
(3)考察函数y=
的图象.当x=-2时,y= ;当x<-2时,y的取值范围是 ;当y>-1时,y的取值范围是 ;
(4)计算sin230°+2sin60°+tan45°-tan60°+cos230°= ;
(5)将y=3x2向 平移 个单位得到y=3(x+1)2,对称轴是 ,当 时,y的值随x的值增大而增大.
(1)函数y=-x上的点的坐标和为
(2)函数y=x+1与x轴所夹的锐角为
(3)考察函数y=
| 2 |
| x |
(4)计算sin230°+2sin60°+tan45°-tan60°+cos230°=
(5)将y=3x2向
考点:一次函数图象上点的坐标特征,反比例函数的性质,二次函数图象与几何变换,特殊角的三角函数值
专题:
分析:(1)根据函数y=-x上横纵坐标的特点进行解答即可.
(2)求出直线与两坐标轴的交点,再根据锐角三角函数的定义即可得出结论;
(3)直接吧x=-2代入函数y=
求出y的值;再根据函数的增减性进行解答即可;
(4)分别把各特殊角的三角函数值代入进行计算即可;
(5)直接根据图形平移的性质及二次函数的性质进行解答即可.
(2)求出直线与两坐标轴的交点,再根据锐角三角函数的定义即可得出结论;
(3)直接吧x=-2代入函数y=
| 2 |
| x |
(4)分别把各特殊角的三角函数值代入进行计算即可;
(5)直接根据图形平移的性质及二次函数的性质进行解答即可.
解答:解:(1)∵函数y=-x上横纵坐标互为相反数,
∴函数y=-x上的点的坐标和0.
故答案为:0;
(2)∵当x=0时,y=1,当y=0时,x=-1,
∴函数y=x+1与两坐标轴的交点分别为(0,1),(-1,0),
∴tanα=1,
∴函数y=x+1与x轴所夹的锐角为45°.
故答案为:45°;
(3)当x=-2时,y=-1,
∵k=2>0,
∴此函数的图象在第三象限中y随x的增大而减小,
∴当x<-2时,y>-1,当y>-1时,x<-2.
故答案为:-1,y>-1,x<-2;
(4)原式=
+2×
+1-
+
=
+
+1-
+
=2.
故答案为:2;
(5)由“左加右减”的法则可知,将将y=3x2向左平移1个单位得到y=3(x+1)2,
∵当x+1=0时,x=-1,
∴对称轴是x=-1,当x>-1时,y的值随x的值增大而增大.
故答案分别为:左,1,x=-1,x>-1.
∴函数y=-x上的点的坐标和0.
故答案为:0;
(2)∵当x=0时,y=1,当y=0时,x=-1,
∴函数y=x+1与两坐标轴的交点分别为(0,1),(-1,0),
∴tanα=1,
∴函数y=x+1与x轴所夹的锐角为45°.
故答案为:45°;
(3)当x=-2时,y=-1,
∵k=2>0,
∴此函数的图象在第三象限中y随x的增大而减小,
∴当x<-2时,y>-1,当y>-1时,x<-2.
故答案为:-1,y>-1,x<-2;
(4)原式=
| 1 |
| 4 |
| ||
| 2 |
| 3 |
| 3 |
| 4 |
=
| 1 |
| 4 |
| 3 |
| 3 |
| 3 |
| 4 |
=2.
故答案为:2;
(5)由“左加右减”的法则可知,将将y=3x2向左平移1个单位得到y=3(x+1)2,
∵当x+1=0时,x=-1,
∴对称轴是x=-1,当x>-1时,y的值随x的值增大而增大.
故答案分别为:左,1,x=-1,x>-1.
点评:本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
在共有25人参加的“校园歌手”比赛中,参赛选手要想知道自己是否能进入前12名,只需要了解自己的成绩及全部成绩的( )
| A、平均数 | B、众数 |
| C、中位数 | D、方差 |
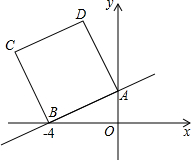 如图,已知直线y=
如图,已知直线y=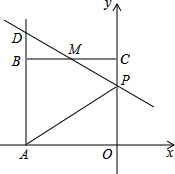 如图,已知正方形OABC的边长为2,顶点A、C分别在x轴的负半轴和y轴的正半轴上,M是BC的中点.P(0,m)是线段OC上一动点(C点除外),直线PM交AB的延长线于点D.
如图,已知正方形OABC的边长为2,顶点A、C分别在x轴的负半轴和y轴的正半轴上,M是BC的中点.P(0,m)是线段OC上一动点(C点除外),直线PM交AB的延长线于点D.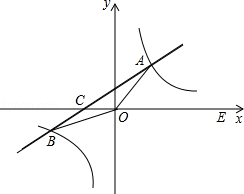 如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=
如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=