题目内容
等腰三角形底边长是10，周长是40，则其底角的正弦值是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点：解直角三角形,等腰三角形的性质
专题：
分析：先求出腰长，作底边上的高，根据三角函数的定义求解．
解答：
解：如图所示：
∵AB=AC，BC=10，AD为底边上的高，周长为40，
∴AB=AC=（40-10）÷2=15．
∵BD=5，
∴由勾股定理得，AD=
=
=10
，
∴tan∠ABC=
=
=
．
故选B．
解：如图所示：∵AB=AC，BC=10，AD为底边上的高，周长为40，
∴AB=AC=（40-10）÷2=15．
∵BD=5，
∴由勾股定理得，AD=
| AB2-BD2 |
| 152-52 |
| 2 |
∴tan∠ABC=
| AD |
| AB |
10
| ||
| 15 |
2
| ||
| 3 |
故选B．
点评：本题考查的是解直角三角形，熟知锐角三角函数的定义是解答此题的关键．
练习册系列答案
相关题目
如图，?ABCD的周长是36cm，AB=8cm，BC=
?ABCD中，DE平分∠ADC，交AB于E，AD=7，BE=2，则?ABCD的周长为
如图，是一块电脑主板的示意图，每一转角处都是直角，数据如图（单位：mm），则该主板的周长是（ ）| A、88mm | B、96mm |
| C、80mm | D、84mm |
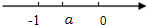实数a在数轴上的位置如图，则a，-a，| 1 |
| a |
A、a＜-a＜
| ||
B、-a＜
| ||
C、
| ||
D、
|
在△ABC中，∠C=90°，a=8，b=15，sinA+sinB等于（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知24+n•42n+1=（
）-n，则n为（ ）
| 1 |
| 8 |
| A、n=-3 | B、n=-2 |
| C、n=-1 | D、n=0 |
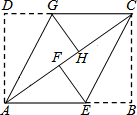如图，ABCD是矩形纸片，翻折∠B、∠D，使BC，AD恰好落在AC上，其中F，H分别是B，D的落点．求证：四边形AECG是平行四边形．