题目内容
7.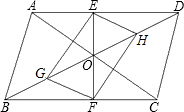 如图,在?ABCD中,对角线AC、BD相交于点O,已知E、F、G、H分别是BC、AD、OB、OD的中点,试说明四边形EGFH是平行四边形.
如图,在?ABCD中,对角线AC、BD相交于点O,已知E、F、G、H分别是BC、AD、OB、OD的中点,试说明四边形EGFH是平行四边形.
分析 对角线互相平分的四边形是平行四边形,在本题中,OG=OH可以根据线段之间的等量关系求出,而OE=OF则需通过证明全等得出.解本题则可利用这一判定,利用全等证明OE=OF即可.
解答 解:∵四边形ABCD为平行四边形,
∴BO=DO,AD=BC且AD∥BC,
∴∠ADO=∠CBO,
在△FOB与△EOD中,
$\left\{\begin{array}{l}{∠ADO=∠CBO}\\{OB=OD}\\{∠DOE=∠FOB}\\{\;}\end{array}\right.$,
∴△FOB≌△EOD(ASA),
∴EO=FO,
又∵G、H分别为OB、OD的中点,
∴GO=HO,
∴四边形EFGH为平行四边形.
点评 本题考查了平行四边形的判定与性质,全等三角形的判定和性质,熟练掌握性质定理和判定定理是解题的关键.平行四边形的五种判定方法与平行四边形的性质相呼应,每种方法都对应着一种性质,在应用时应注意它们的区别与联系.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
12.已知$\frac{a}{b}=\frac{2}{3}$,那么$\frac{a+b}{b}$=( )
| A. | $\frac{5}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{2}$ | D. | $\frac{3}{5}$ |
19. 如图:在△ABC中,∠ACB=90°,AC=BC,⊙O与AB相切,且点0到直线AB的距离等于△ABC中AB边上的高,与边AC,BC分别相交于点M,N,若⊙0半径为2,当⊙0在边AB上滚动时,则$\widehat{MN}$的长为( )
如图:在△ABC中,∠ACB=90°,AC=BC,⊙O与AB相切,且点0到直线AB的距离等于△ABC中AB边上的高,与边AC,BC分别相交于点M,N,若⊙0半径为2,当⊙0在边AB上滚动时,则$\widehat{MN}$的长为( )
 如图:在△ABC中,∠ACB=90°,AC=BC,⊙O与AB相切,且点0到直线AB的距离等于△ABC中AB边上的高,与边AC,BC分别相交于点M,N,若⊙0半径为2,当⊙0在边AB上滚动时,则$\widehat{MN}$的长为( )
如图:在△ABC中,∠ACB=90°,AC=BC,⊙O与AB相切,且点0到直线AB的距离等于△ABC中AB边上的高,与边AC,BC分别相交于点M,N,若⊙0半径为2,当⊙0在边AB上滚动时,则$\widehat{MN}$的长为( )| A. | $\frac{1}{2}$π | B. | $\frac{\sqrt{3}}{2}$π | C. | π | D. | 无法确定 |
16.下列各式中,正确的是( )
| A. | $\sqrt{9}$=±3 | B. | ±$\sqrt{25}$=5 | C. | $\sqrt{{{(-3)}^2}}$=-3 | D. | $\root{3}{-27}$=-3 |
17.下列式子正确的是( )
| A. | -3>0 | B. | -0.1>-0.01 | C. | |-2|<|-4| | D. | |-5|<4 |




 如图,BP是△ABC的内角∠ABC的角平分线,交外角∠ACD的角平分线CP于点P,已知∠A=70°,则∠P的度数为35°.
如图,BP是△ABC的内角∠ABC的角平分线,交外角∠ACD的角平分线CP于点P,已知∠A=70°,则∠P的度数为35°.