题目内容
19.将抛物线y=mx2+n向下平移6个单位长度,得到抛物线y=-x2+3,设原抛物线的顶点为P,且原抛物线与x轴相交于点A、B,求△PAB的面积.分析 根据平移的性质得出y=mx2+n-6,根据题意求得m=-1,n=9,从而求得原抛物线的解析式,得出顶点坐标和与x轴的交点坐标,进而根据三角形面积求得即可.
解答 解:∵将抛物线y=mx2+n向下平移6个单位长度,得到y=mx2+n-6,
∴m=-1,n-6=3,
∴n=9,
∴原抛物线y=-x2+9,
∴顶点P(0,6),
令y=0,则0=-x2+9,
解得x=±3,
∴A(-3,0),B(3,0),
∴AB=6,
∴S△PAB=$\frac{1}{2}$AB•OP=$\frac{1}{2}$×6×6=18.
点评 本题考查了二次函数图象与几何变换,求得原抛物线的解析式是解题的关键.

练习册系列答案
相关题目
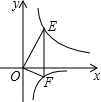 如图,直线EF∥y轴,分别交双曲线y=$\frac{8}{x}$(x>0和y=-$\frac{2}{x}$(x>0)的图象于E、F,且OE⊥OF,则EF=5.
如图,直线EF∥y轴,分别交双曲线y=$\frac{8}{x}$(x>0和y=-$\frac{2}{x}$(x>0)的图象于E、F,且OE⊥OF,则EF=5. 如图是一个由多个相同小正方体堆积而成的几何体从上面看到的形状图,图中所示数字为该位置小正方形的个数,请你画出它从正面和从左面看到的形状图.
如图是一个由多个相同小正方体堆积而成的几何体从上面看到的形状图,图中所示数字为该位置小正方形的个数,请你画出它从正面和从左面看到的形状图.