题目内容
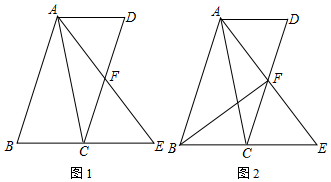
11.已知,如图,在四边形ABCD中,AB∥CD,延长BC至点E,连接AE交CD于点F,使∠BAC=∠DAE,∠ACB=∠CFE(1)求证:∠BAF=∠CAD;
(2)求证:AD∥BE;
(3)若BF平分∠ABC,请写出∠AFB与∠CAF的数量关系2∠AFB+∠CAF=180°..(不需证明)
分析 (1)根据∠BAC=∠DAE,运用等式性质即可得出∠BAC+∠CAF=∠DAE+∠CAF,进而得到∠BAF=∠CAD;
(2)根据∠BAC=∠DAF,∠ACB=∠CFE=∠AFD,可得∠B=∠D,最后根据∠B+∠BCD=180°,可得∠D+∠BCD=180°,进而判定AD∥BE;
(3)根据AD∥BE,可得∠E=∠1=∠2,再根据BF平分∠ABC,可得∠3=∠4,根据∠AFB是△BEF的外角,得出∠AFB=∠4+∠E=∠4+∠1,即∠AFB=3+∠2,最后根据AD∥BC,得到∠ABC+∠BAD=180°,进而得到2∠AFB+∠CAF=180°.
解答  解:(1)∵∠BAC=∠DAE,
解:(1)∵∠BAC=∠DAE,
∴∠BAC+∠CAF=∠DAE+∠CAF,
∴∠BAF=∠CAD;
(2)∵∠BAC=∠DAF,∠ACB=∠CFE=∠AFD,
∴∠B=∠D,
∵AB∥CD,
∴∠B+∠BCD=180°,
∴∠D+∠BCD=180°,
∴AD∥BE;
(3)如图2,∵AD∥BE,
∴∠E=∠1=∠2,
∵BF平分∠ABC,
∴∠3=∠4,
∵∠AFB是△BEF的外角,
∴∠AFB=∠4+∠E=∠4+∠1,
∴∠AFB=3+∠2,
又∵AD∥BC,
∴∠ABC+∠BAD=180°,
∴∠3+∠4+∠1+∠CAF+∠2=180°,
即2∠AFB+∠CAF=180°.
故答案为:2∠AFB+∠CAF=180°.
点评 本题主要考查了平行线的性质与判定,三角形外角性质,角平分线的定义以及三角形内角和定理的综合应用,解题时注意:平行线的判定是由角的数量关系判断两直线的位置关系,平行线的性质是由平行关系来寻找角的数量关系.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
2.下列二次根式中是最简二次根式的是( )
| A. | $\sqrt{4}$ | B. | $\sqrt{8}$ | C. | $\sqrt{10}$ | D. | $\sqrt{12}$ |
19.下列命题错误的是( )
| A. | 平行四边形的对角线互相平分 | |
| B. | 矩形的对角线相等 | |
| C. | 对角线互相垂直平分的四边形是菱形 | |
| D. | 对角线相等的四边形是矩形 |
6.下列命题是假命题的有( )
①邻补角相等;②对顶角相等;③同位角相等;④内错角相等.
①邻补角相等;②对顶角相等;③同位角相等;④内错角相等.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3. 如图所示的几何体的俯视图是( )
如图所示的几何体的俯视图是( )
 如图所示的几何体的俯视图是( )
如图所示的几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |

 如图,点A、D、C、E在同一条直线上,AB∥EF,AB=EF,∠B=∠F,AE=10,AC=6,则CD的长为2.
如图,点A、D、C、E在同一条直线上,AB∥EF,AB=EF,∠B=∠F,AE=10,AC=6,则CD的长为2.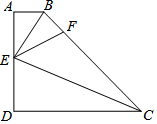 如图,在四边形ABCD中,AB∥CD,∠D=90°,E为AD上一点,分别以EB,EC为折痕将这两个角(∠A,∠D)向内折起,点A,D恰好落在BC边的F处,若AB=1,DC=4,则△EBC的面积为5.
如图,在四边形ABCD中,AB∥CD,∠D=90°,E为AD上一点,分别以EB,EC为折痕将这两个角(∠A,∠D)向内折起,点A,D恰好落在BC边的F处,若AB=1,DC=4,则△EBC的面积为5.