题目内容
函数y=ax2+bx+c的图象如图，那么关于x的一元二次方程ax2+bx+c-4=0的根的情况是考点：抛物线与x轴的交点
专题：
分析：由图可知ax2+bx+c-2=0的根的情况即图中图象和x轴交点的横坐标，为两个不相等的正数，再根据y=ax2+bx+c-4，相当于函数y=ax2+bx+c的图象向下平移4个单位，由此可得出结论．
解答：解：∵函数的顶点的纵坐标为3，
∴直线y=3与函数图象只有一个交点，
∴y=ax2+bx+c-4，相当于函数y=ax2+bx+c的图象向下平移4个单位，
∴方程ax2+bx+c-4=0没有实数根．
故答案为：没有实数根．
∴直线y=3与函数图象只有一个交点，
∴y=ax2+bx+c-4，相当于函数y=ax2+bx+c的图象向下平移4个单位，
∴方程ax2+bx+c-4=0没有实数根．
故答案为：没有实数根．
点评：本题考查了二次函数与一元二次方程的知识，解题的关键是通过看图象直线y=3与抛物线的交点个数．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，在△ABC中，AB=AC=10，BC=12，矩形DEFG的顶点位于△ABC的边上，设EF=x，S四边形DEFG=y，写出y与x的函数表达式，并列出表格，画出相应的函数图象，根据这三种表示方式回答下列问题：
如图，已知二次函数y=ax2+2x+c（a＞0）图象的顶点M在反比例函数y=
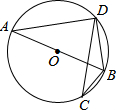如图，已知⊙O是△ABD的外接圆，AB是⊙O的直径，CD是⊙O的弦，∠ABD=56°，则∠BCD等于（ ）| A、112° | B、34° |
| C、56° | D、68° |
如图所示的标志中，不是轴对称图形的有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |