题目内容
16.估计7-$\sqrt{5}$的值在( )| A. | 2到3之间 | B. | 3到4之间 | C. | 4到5之间 | D. | 5到6之间 |
分析 根据被开方数越大算术平方根跟越大,可得答案.
解答 解:∵2<$\sqrt{5}$<3,
∴-3<-$\sqrt{5}$<-2,
∴4<7-$\sqrt{5}$<5,
故选:C.
点评 本题考查了估算无理数的大小,利用被开方数越大算术平方根跟越大得出2<$\sqrt{5}$<3是解题关键.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
6. 如图,在直角坐标系中,点A、B分别在x轴,y轴上,点A的坐标为(-2,0),∠ABO=30°,线段PQ的端点P从点O出发,沿△OBA的边按O→B→A→O运动一周,同时另一端点Q随之在x轴的非负半轴上运动,如果PQ=2$\sqrt{3}$,那么当点P运动一周时,点Q运动的总路程为( )
如图,在直角坐标系中,点A、B分别在x轴,y轴上,点A的坐标为(-2,0),∠ABO=30°,线段PQ的端点P从点O出发,沿△OBA的边按O→B→A→O运动一周,同时另一端点Q随之在x轴的非负半轴上运动,如果PQ=2$\sqrt{3}$,那么当点P运动一周时,点Q运动的总路程为( )
 如图,在直角坐标系中,点A、B分别在x轴,y轴上,点A的坐标为(-2,0),∠ABO=30°,线段PQ的端点P从点O出发,沿△OBA的边按O→B→A→O运动一周,同时另一端点Q随之在x轴的非负半轴上运动,如果PQ=2$\sqrt{3}$,那么当点P运动一周时,点Q运动的总路程为( )
如图,在直角坐标系中,点A、B分别在x轴,y轴上,点A的坐标为(-2,0),∠ABO=30°,线段PQ的端点P从点O出发,沿△OBA的边按O→B→A→O运动一周,同时另一端点Q随之在x轴的非负半轴上运动,如果PQ=2$\sqrt{3}$,那么当点P运动一周时,点Q运动的总路程为( )| A. | 6 | B. | 6+2$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 8 |
11.下列说法正确的是( )
| A. | 了解我国青年人喜欢的电视节目应采用全面调查 | |
| B. | 对飞机乘客的安检应采用抽样调查 | |
| C. | “掷一次硬币,出现正面向上”是随机事件 | |
| D. | “购买1张彩票就中奖”是不可能事件 |
8.直线y=-2(x-1)+1与水平线所夹锐角的余弦是( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | -$\frac{\sqrt{5}}{5}$ |
6.某工厂生产一种合金薄板(其厚度忽略不计)这些薄板的形状均为正方形,边长(单位:cm)在5~50之间,每张薄板的成本价(单位:元)与它的面积(单位:cm2)成正比例,每张薄板的出厂价(单位:元)由基础价和浮动价两部分组成,(即出厂价=基础价+浮动价)其中基础价与薄板的大小无关,是固定不变的,浮动价与薄板的边长x成正比例,在营销过程中得到了表格中的数据,已知出厂一张边长为40cm的薄板,获得利润是26元.(利润=出厂价-成本价)
(1)求一张薄板的出厂价y与边长x之间满足的函数关系式;
(2)求一张薄板的利润p与边长x之间的函数关系式;
(3)若一张薄板的利润是34元,且成本最低,此时薄板的边长为多少?当薄板的边长为多少时,所获利润最大,求出这个最大值.
| 薄板的边长(cm) | 20 | 30 |
| 出厂价(元/张) | 50 | 70 |
(2)求一张薄板的利润p与边长x之间的函数关系式;
(3)若一张薄板的利润是34元,且成本最低,此时薄板的边长为多少?当薄板的边长为多少时,所获利润最大,求出这个最大值.
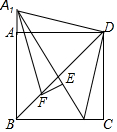 如图,在正方形ABCD中,点C1在边BC上,将△C1CD绕点D顺时针旋转90°得到△A1AD.A1F平分∠BA1C1,交BD于点F,过点F作FE⊥A1C1,垂足为E,当A1E=3,C1E=2时,则BD的长为$\frac{7\sqrt{2}}{2}$.
如图,在正方形ABCD中,点C1在边BC上,将△C1CD绕点D顺时针旋转90°得到△A1AD.A1F平分∠BA1C1,交BD于点F,过点F作FE⊥A1C1,垂足为E,当A1E=3,C1E=2时,则BD的长为$\frac{7\sqrt{2}}{2}$.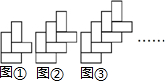 用长为2cm、宽为1cm的矩形无缝隙的摆出如图所示的图形,图形①由4个矩形组成,其外轮廓(即图形的周长)为14cm,图形②由6个矩形组成,图形③由8个矩形组成…以此类推,则图形⑨的外轮廓为46cm.
用长为2cm、宽为1cm的矩形无缝隙的摆出如图所示的图形,图形①由4个矩形组成,其外轮廓(即图形的周长)为14cm,图形②由6个矩形组成,图形③由8个矩形组成…以此类推,则图形⑨的外轮廓为46cm.