题目内容
1.下列各数中,绝对值最大的数是( )| A. | 1 | B. | 0 | C. | -3 | D. | -2 |
分析 首先根据绝对值的含义和求法,分别求出每个数的绝对值各是多少;然后根据有理数大小比较的法则:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小,判断出各数中,绝对值最大的数是哪个即可.
解答 解:|1|=1,|0|=0,|-3|=3,|-2|=2,
∵3>2>1>0,
∴各数中,绝对值最大的数是-3.
故选:C.
点评 (1)此题主要考查了有理数大小比较的方法,要熟练掌握,解答此题的关键是要明确:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小.
(2)此题还考查了绝对值的含义和应用,要熟练掌握,解答此题的关键是要明确:①当a是正有理数时,a的绝对值是它本身a;②当a是负有理数时,a的绝对值是它的相反数-a;③当a是零时,a的绝对值是零.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
11. 如图,在菱形ABCD中,点O在对角线AC上,且AO=2CO,连接OB、OD,若OB=OC=OD,AC=3,则菱形的边长为( )
如图,在菱形ABCD中,点O在对角线AC上,且AO=2CO,连接OB、OD,若OB=OC=OD,AC=3,则菱形的边长为( )
 如图,在菱形ABCD中,点O在对角线AC上,且AO=2CO,连接OB、OD,若OB=OC=OD,AC=3,则菱形的边长为( )
如图,在菱形ABCD中,点O在对角线AC上,且AO=2CO,连接OB、OD,若OB=OC=OD,AC=3,则菱形的边长为( )| A. | $\sqrt{3}$ | B. | 2 | C. | $\frac{\sqrt{5}+1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
12.某校组织1080名学生去外地参观,现有A、B两种不同型号的客车可供选择.在每辆车刚好满座的前提下,每辆B型客车比每辆A型客车多坐15人,单独选择B型客车比单独选择A型客车少租12辆,设A型客车每辆坐x人,根据题意列方程为( )
| A. | $\frac{1080}{x}=\frac{1080}{x-15}+12$ | B. | $\frac{1080}{x}=\frac{1080}{x-15}-12$ | ||
| C. | $\frac{1080}{x}=\frac{1080}{x+15}-12$ | D. | $\frac{1080}{x}=\frac{1080}{x+15}+12$ |
16.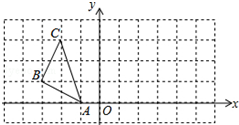 如图,△ABC的三个顶点都在方格纸的格点上,其中点A的坐标是(-1,0).现将△ABC绕点A顺时针旋转90°,则旋转后点C的坐标是( )
如图,△ABC的三个顶点都在方格纸的格点上,其中点A的坐标是(-1,0).现将△ABC绕点A顺时针旋转90°,则旋转后点C的坐标是( )
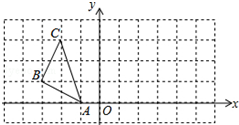 如图,△ABC的三个顶点都在方格纸的格点上,其中点A的坐标是(-1,0).现将△ABC绕点A顺时针旋转90°,则旋转后点C的坐标是( )
如图,△ABC的三个顶点都在方格纸的格点上,其中点A的坐标是(-1,0).现将△ABC绕点A顺时针旋转90°,则旋转后点C的坐标是( )| A. | (2,1) | B. | (1,2) | C. | (-2,-1) | D. | (-1,-2) |
6.如图,填在各方格中的三个数之间均具有相同的规律,据此规律,n的值是( )


| A. | 48 | B. | 56 | C. | 63 | D. | 74 |
13.计算(-2a3)2的结果是( )
| A. | -8a5 | B. | 4a6 | C. | 8a5 | D. | -4a6 |
11. 如图,AB是⊙O的弦,半径OC⊥AB于点D,且AB=8,OC=5,则OD的长为( )
如图,AB是⊙O的弦,半径OC⊥AB于点D,且AB=8,OC=5,则OD的长为( )
 如图,AB是⊙O的弦,半径OC⊥AB于点D,且AB=8,OC=5,则OD的长为( )
如图,AB是⊙O的弦,半径OC⊥AB于点D,且AB=8,OC=5,则OD的长为( )| A. | 1 | B. | 2 | C. | 2.5 | D. | 3 |