题目内容
(1)数学课上,老师出了一道题,如图①,Rt△ABC中,∠C=90°,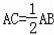
 ,求证:∠B=30°,请你完成证明过程.
,求证:∠B=30°,请你完成证明过程.
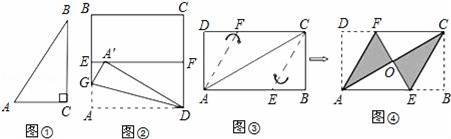
(2)如图②,四边形ABCD是一张边长为2的正方形纸片,E、F分别为AB、CD的中点,沿过点D的抓痕将纸片翻折,使点A落在EF上的点A′处,折痕交AE于点G,请运用(1)中的结论求∠ADG的度数和AG的长.
(3)若矩形纸片ABCD按如图③所示的方式折叠,B、D两点恰好重合于一点O(如图④),当AB=6,求EF的长.

【考点】翻折变换(折叠问题).
【专题】压轴题.
【分析】(1)Rt△ABC中,根据sinB═
 =
=
 ,即可证明∠B=30°;
,即可证明∠B=30°;
(2)求出∠FA′D的度数,利用翻折变换的性质可求出∠ADG的度数,在Rt△A'FD中求出A'F,得出A'E,在Rt△A'EG中可求出A'G,利用翻折变换的性质可得出AG的长度.
(3)先判断出AD=
 AC,得出∠ACD=30°,∠DAC=60°,从而求出AD的长度,根据翻折变换的性质可得出∠DAF=∠FAO=30°,在Rt△ADF中求出DF,继而得出FO,同理可求出EO,再由EF=EO+FO,即可得出答案.
AC,得出∠ACD=30°,∠DAC=60°,从而求出AD的长度,根据翻折变换的性质可得出∠DAF=∠FAO=30°,在Rt△ADF中求出DF,继而得出FO,同理可求出EO,再由EF=EO+FO,即可得出答案.
【解答】(1)证明:Rt△ABC中,∠C=90°,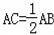
 ,
,
∵sinB=
 =
=
 ,
,
∴∠B=30°;
(2)解:∵正方形边长为2,E、F为AB、CD的中点,
∴EA=FD=
 ×边长=1,
×边长=1,
∵沿过点D的抓痕将纸片翻折,使点A落在EF上的点A′处,
∴A′D=AD=2,
∴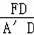
 =
=
 ,
,
∴∠FA′D=30°,
可得∠FDA′=90°﹣30°=60°,
∵A沿GD折叠落在A′处,
∴∠ADG=∠A′DG,AG=A′G,
∴∠ADG=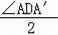
 =
=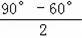
 =15°,
=15°,
∵A′D=2,FD=1,
∴A′F=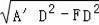
 =
=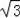
 ,
,
∴EA′=EF﹣A′F=2﹣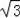
 ,
,
∵∠EA′G+∠DA′F=180°﹣∠GA′D=90°,
∴∠EA′G=90°﹣∠DA′F=90°﹣30°=60°,
∴∠EGA′=90°﹣∠EA′G=90°﹣60°=30°,
则A′G=AG=2EA′=2(2﹣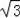
 );
);
(3)解:∵折叠后B、D两点恰好重合于一点O,
∴AO=AD=CB=CO,
∴DA=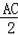
 ,
,
∵∠D=90°,
∴∠DCA=30°,
∵AB=CD=6,
在Rt△ACD中,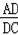
 =tan30°,
=tan30°,
则AD=DC•tan30°=6×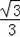
 =2
=2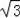
 ,
,
∵∠DAF=∠FAO=
 ∠DAO=
∠DAO=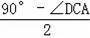
 =30°,
=30°,
∴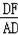
 =tan30°=
=tan30°=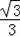
 ,
,
∴DF=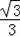
 AD=2,
AD=2,
∴DF=FO=2,
同理EO=2,
∴EF=EO+FO=4.
【点评】本题考查了翻折变换的知识,涉及了含30°角的直角三角形的性质、平行四边形的性质,综合考察的知识点较多,注意将所学知识融会贯通.


 B.
B.
 C.
C.
 D.
D.


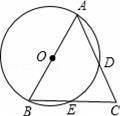





 米,则这个坡面的坡度为( )
米,则这个坡面的坡度为( )


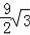
 )米2 B.(π﹣
)米2 B.(π﹣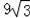
 )米2
)米2

 [6+(﹣3)3].
[6+(﹣3)3].