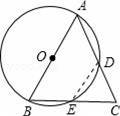
题目内容
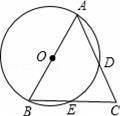
如图,在△ABC中,AB=AC=
 ,BC=2,以AB为直径的⊙O分别交AC、BC两边于点D、E,则△CDE的面积为 .
,BC=2,以AB为直径的⊙O分别交AC、BC两边于点D、E,则△CDE的面积为 .

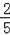
 .
.
【考点】相似三角形的判定与性质;等腰三角形的性质;勾股定理;圆周角定理.
【分析】连接DE,由∠B+∠ADE=180°,∠ADE+∠EDC=180°得∠B=∠EDC,证△EDC∽△ABC,则再由相似三角形的面积之比等于边长比的平方.
【解答】解:连接DE.
在⊙O中,∠B+∠ADE=180°,又∠ADE+∠EDC=180°,
则∠B=∠EDC,∠ACB=∠ECD,△EDC∽△ABC,
由于AB为直径,AB=AC,则AE⊥BC,E为BC中点,EC=1,AE=2
则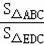
 =
=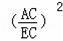
 =5.
=5.
∵S△ABC=
 ×2×2=2,
×2×2=2,
∴S△EDC=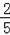
 .
.

【点评】本题考查了相似三角形的性质,面积之比等于对应边之比的平方.

练习册系列答案
相关题目
 =3,则
=3,则 =( )
=( ) B.xy C.4 D.
B.xy C.4 D.

 B.
B.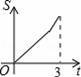
 C.
C.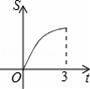
 D.
D.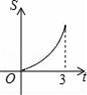

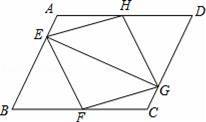

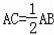
 ,求证:∠B=30°,请你完成证明过程.
,求证:∠B=30°,请你完成证明过程.

 x2+
x2+
 x(x>0),若该车某次的刹车距离为9m,则开始刹车时的速度为 m/s.
x(x>0),若该车某次的刹车距离为9m,则开始刹车时的速度为 m/s.
