题目内容
9. A点坐标为-20,C点坐标为40,一只电子蚂蚁甲从C点出发向左移动,速度为2个单位长度/秒.B为数轴上(线段AC之间)一动点,D为BC的中点.
A点坐标为-20,C点坐标为40,一只电子蚂蚁甲从C点出发向左移动,速度为2个单位长度/秒.B为数轴上(线段AC之间)一动点,D为BC的中点.(1)这只电子蚂蚁甲由D点走到AB的中点E处,需要几秒钟?
(2)在(1)的条件下,当电子蚂蚁甲从E点返回时,另一只蚂蚁乙同时从C点出发向左移动,速度为3个单位长度/秒,如果两只蚂蚁相遇于H点离B点5个单位长度,求B点对应的数.
分析 (1)根据A,B两处的距离之和是BD+DA=DC+DA=AC,根据D、E分别是AB、BC的中点,求出DE,再根据这只电子蚂蚁移动速度为每秒2个单位长度列式计算即可;
(2)设B点的位置为m,相遇点为F,然后分两种情况进行讨论:①点F在线段AB上离B点5个单位长度处;②点F在线段BC上离B点5个单位长度处.
解答 解:(1)A,B两处的距离之和是:BD+DA=DC+DA=AC=40+20=60;
∵D、E分别是AB、BC的中点,
∴DE=$\frac{1}{2}$AC=$\frac{1}{2}$×60=30,
∴这只电子蚂蚁甲由D点走到AB的中点E处需要的时间是:
30÷2=15(秒).
答:这只电子蚂蚁甲由D点走到AB的中点E处需要15秒钟;
(2)设B点的位置为m,相遇点为F,
①点F在线段AB上离B点5个单位长度处,依题意有
[$\frac{1}{2}$(m+20)-5]:(40-m+5)=2:3,
解得m=21$\frac{3}{7}$;
②点F在线段BC上离B点5个单位长度处,依题意有
[$\frac{1}{2}$(m+20)+5]:(40-m-5)=2:3,
解得m=7$\frac{1}{7}$.
故B点的位置为21$\frac{3}{7}$或7$\frac{1}{7}$.
点评 此题考查了一元一次方程的应用和数轴,用到的知识点是线段的中点、速度时间路程之间的关系,关键是根据线段的中点求出线段的长度.

练习册系列答案
相关题目
19.2x3y2与12x6y的公因式是( )
| A. | xy | B. | x3y | C. | 2x3y | D. | 12x6y2 |
4.一个扇形的圆心角所对的弧长是所在圆周长的$\frac{5}{12}$,已知扇形面积是35cm2,那么下列相关列式中错误的是( )
| A. | $\frac{360}{n}$=$\frac{12}{5}$ | B. | $\frac{35}{{S}_{面}}$=$\frac{5}{12}$ | C. | $\frac{5}{12}$=$\frac{n}{180}$ | D. | S面=35$÷\frac{5}{12}$ |
1.9的平方根是( )
| A. | 3 | B. | -3 | C. | ±3 | D. | 9 |
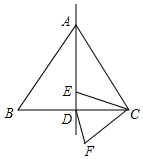 如图,△ABC是边长为12的等边三角形,D是BC的中点,E是直线AD上的一个动点,连接EC,将线段EC绕点C逆时针旋转60°得到FC,连接DF.则在点E的运动过程中,DF的最小值是3.
如图,△ABC是边长为12的等边三角形,D是BC的中点,E是直线AD上的一个动点,连接EC,将线段EC绕点C逆时针旋转60°得到FC,连接DF.则在点E的运动过程中,DF的最小值是3.