题目内容
若m1、m2、n1、n2是实数，且m1m2=2（n1+n2）．求证：方程x2+m1x+n1=0和方程x2+m2x+n2=0中至少有一个方程有实数根．
考点：根的判别式
专题：证明题
分析：首先分别求出两个方程的判别式，然后把它们相加，接着利用m1m2=2（n1+n2）证明它们的和是非负数，根据判别式与方程的根的关系即可解决问题．
解答：解：∵方程x2+m1x+n1=0的判别式为△1=m12-4n1，
方程x2+m2x+n2=0的判别式为△2=m22-4n2，
∴△1+△2=m12-4n1+m22-4n2=m12+m22-4（n1+n2），
∵m1m2=2（n1+n2），
∴△1+△2=m12+m22-2m1m2=（m1-m2）2≥0，
∴△1和△2中至少有一个正数或都是0，
∴方程x2+m1x+n1=0和方程x2+m2x+n2=0中至少有一个方程有实数根．
方程x2+m2x+n2=0的判别式为△2=m22-4n2，
∴△1+△2=m12-4n1+m22-4n2=m12+m22-4（n1+n2），
∵m1m2=2（n1+n2），
∴△1+△2=m12+m22-2m1m2=（m1-m2）2≥0，
∴△1和△2中至少有一个正数或都是0，
∴方程x2+m1x+n1=0和方程x2+m2x+n2=0中至少有一个方程有实数根．
点评：此题考查了一元二次方程的根和判别式之间的关系，若△＞0，则方程有两个不相等的实数根；若△=0，则方程有两个相等的实数根；若△＜0，则方程没有实数根．
练习册系列答案
名校课堂系列答案
相关题目
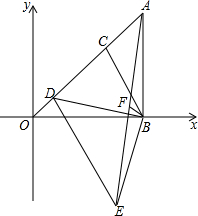直角坐标系中，直线OC和BC的函数关系式分别是y=x，y=-2x+6，过B点作x轴的垂线交直线OC于A点，D是线段OC上的一个动点（点D，O不重合），以BD为直角边作等腰Rt△BDE（E在第四象限），F是AE中点．确定线段BF、AD的数量关系和位置关系，并加以证明．