题目内容
2.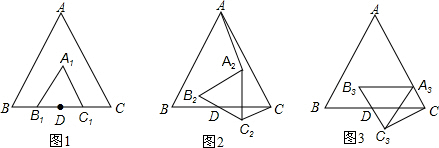 已知,△ABC和△A1B1C1均为正三角形,BC和B1C1的中点均为D,如图1.
已知,△ABC和△A1B1C1均为正三角形,BC和B1C1的中点均为D,如图1.(1)当△A1B1C1绕点D旋转到△A2B2C2时,试判断AA2与CC2的位置关系,并证明你的结论.
(2)如果当△A1B1C1绕点D旋转一周,顶点A1和AC仅有一个交点,设该交点为A3,如图3.当AB=4时,求多边形ABDC3C的面积.
分析 (1)利用等边三角形的性质以及结合相似三角形的判定与性质得出得∠A2AD=∠C2CD,进而得出∠ADE=∠CFE=90°,即可得出答案;
(2)首先连接A3D,过C3作C3G⊥BC于G,进而得出C3C,C3G的长,进而利用多边形ABDC3C的面积=S△ABC+S△CC3D,求出答案.
解答 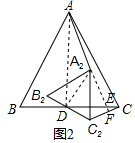 解:(1)AA2⊥CC2
解:(1)AA2⊥CC2
理由:在图2中,连接AD、A2D、延长AA2交BC于E,交CC2于F,
∵BC和B1C1的中点均为D,△A1B1C1绕点D旋转到△A2B2C2,
∴∠ADA2=90°-∠A2DC=∠CDC2,$\frac{AD}{{D{A_2}}}=\frac{DC}{{D{C_2}}}$,(等边三角形都相似,相似三角形对应高的比等于相似比),
∴△AA2D∽△CC2D,
于是得∠A2AD=∠C2CD,
又∵∠AED=∠CEF,
∴∠ADE=∠CFE=90°,
∴AA2⊥CC2;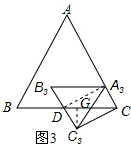
(2)在图3中,连接A3D,过C3作C3G⊥BC于G,由(1)得AC⊥CC3,
由题意得A3D⊥AC,四边形A3CC3D是矩形,
则C3C=A3D=2sin60°=$\sqrt{3}$,
C3G=$\sqrt{3}$sin(90°-60°)=$\frac{\sqrt{3}}{2}$,
故多边形ABDC3C的面积=S△ABC+S△CC3D=$\frac{1}{2}$×4×4sin60°+$\frac{1}{2}$×2×$\frac{\sqrt{3}}{2}$=$\frac{{9\sqrt{3}}}{2}$.
点评 此题主要考查了几何变换以及相似三角形的判定与性质和解直角三角形的应用,正确利用相似三角形的判定与性质是解题关键.

练习册系列答案
相关题目
8.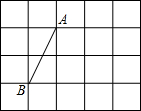 如图,A、B两点均在由小正方形组成的网格格点上,若C点也在格点上,且△ABC是等腰直角三角形,则符合条件的C点的个数有( )
如图,A、B两点均在由小正方形组成的网格格点上,若C点也在格点上,且△ABC是等腰直角三角形,则符合条件的C点的个数有( )
 如图,A、B两点均在由小正方形组成的网格格点上,若C点也在格点上,且△ABC是等腰直角三角形,则符合条件的C点的个数有( )
如图,A、B两点均在由小正方形组成的网格格点上,若C点也在格点上,且△ABC是等腰直角三角形,则符合条件的C点的个数有( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
14.已知a、b、c是三角形的三边,且满足|a-$\frac{3}{2}$|+(b-2)2+$\sqrt{c-\frac{5}{2}}$=0,则这个三角形是( )
| A. | 等腰三角形 | B. | 直角三角形 | C. | 等腰直角三角形 | D. | 钝角三角形 |
11.用总长为60cm的篱笆围成矩形场地.
(Ⅰ)根据题意,填写下表:
(Ⅱ)设矩形一边长为lm,矩形面积为Sm2,当l是多少时,矩形场地的面积S最大?并求出矩形场地的最大面积;
(Ⅱ)当矩形的长为18m,宽为12m时,矩形场地的面积为216m2.
(Ⅰ)根据题意,填写下表:
| 矩形一边长/m | 5 | 10 | 15 | 20 |
| 矩形面积/m2 | 125 | 200 | 225 | 200 |
(Ⅱ)当矩形的长为18m,宽为12m时,矩形场地的面积为216m2.
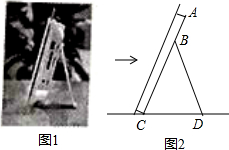 如图1是小红同学书桌上的一个电子相框,将其侧面抽象为如图2所示的几何图形,已知BC=BD=18cm,∠CBD=40°,则点B到CD的距离为16.9cm(用科学计算器计算.参考数据sin20°≈0.342,cos20°≈0.940,sin40°≈0.643,cos40°≈0.766,结果精确到0.1cm).
如图1是小红同学书桌上的一个电子相框,将其侧面抽象为如图2所示的几何图形,已知BC=BD=18cm,∠CBD=40°,则点B到CD的距离为16.9cm(用科学计算器计算.参考数据sin20°≈0.342,cos20°≈0.940,sin40°≈0.643,cos40°≈0.766,结果精确到0.1cm).