题目内容
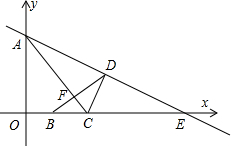 已知抛物线y=ax2+bx+8(a>
已知抛物线y=ax2+bx+8(a>| 1 |
| 2 |
(1)求a、b的值;
(2)设BD与AC交于F,求AF:FC的值.
考点:二次函数综合题
专题:
分析:(1)过点D作DM⊥OE于点M,则DM∥AO,所以△DME∽△AOE,由三角形相似的性质:对应边的比值相等可求出ME的长,再利用已知条件可求出BC的长,进而求出B的坐标,再把B和D的坐标代入抛物线的解析式,即可求出a和b的值;
(2)由(1)中的a=1,b=-6,所以抛物线的解析式可知,进而可得C的坐标,所以直线BD的解析式、直线AC的解析式、直线l的解析式都可求出,再联立直线AC和直线BD的解析式,可求出交点F的坐标,进而可求出AF和FC的值,其比值即可求出.
(2)由(1)中的a=1,b=-6,所以抛物线的解析式可知,进而可得C的坐标,所以直线BD的解析式、直线AC的解析式、直线l的解析式都可求出,再联立直线AC和直线BD的解析式,可求出交点F的坐标,进而可求出AF和FC的值,其比值即可求出.
解答: 解:(1)过点D作DM⊥OE于点M,
解:(1)过点D作DM⊥OE于点M,
∵点D(5,3),
∴OM=5,DM=3,
∵抛物线y=ax2+bx+8(a>
),与y轴交于点A,
∴AO=8,
∵DM∥AO,
∴△DME∽△AOE,
∴
=
,
∴
=
,
解得:ME=3,
∵DM=ME,
∴∠MDE=∠DEM=45°,
∵过点D作直线l⊥CD与y轴交于点A,
∴∠CDM=45°,
∴∠DCM=45°,
∴CM=DM=3,
∵S△ABC=3,
∴
×8×BC=3,
解得:BC=
,
∴B点横坐标为:2,
∴B点坐标为:(2,0),
将B,D点代入函数解析式得:
,
解得:
,
∴a=1,b=-6;
(2)∵a=1,b=-6,
∴抛物线的解析式为:y=x2-6x+8,
∴B(2,0),C(4,0),
∵D(5,3),
∴直线BD为;y=x-2,直线CD为:y=3x-12,
∵直线l⊥CD,
∴直线l的解析式为:y=-
x+b,
把D(5,3)代入得:b=
,
∴直线l的解析式为:y=-
x+
,
∴A(0,
),
∴直线AC为:y=-
x+
,
解;
,得
,
∴F(
,
),
∴
=
=
.
 解:(1)过点D作DM⊥OE于点M,
解:(1)过点D作DM⊥OE于点M,∵点D(5,3),
∴OM=5,DM=3,
∵抛物线y=ax2+bx+8(a>
| 1 |
| 2 |
∴AO=8,
∵DM∥AO,
∴△DME∽△AOE,
∴
| DM |
| AO |
| ME |
| EO |
∴
| 3 |
| 8 |
| ME |
| ME+5 |
解得:ME=3,
∵DM=ME,
∴∠MDE=∠DEM=45°,
∵过点D作直线l⊥CD与y轴交于点A,
∴∠CDM=45°,
∴∠DCM=45°,
∴CM=DM=3,
∵S△ABC=3,
∴
| 1 |
| 2 |
解得:BC=
| 3 |
| 4 |
∴B点横坐标为:2,
∴B点坐标为:(2,0),
将B,D点代入函数解析式得:
|
解得:
|
∴a=1,b=-6;
(2)∵a=1,b=-6,
∴抛物线的解析式为:y=x2-6x+8,
∴B(2,0),C(4,0),
∵D(5,3),
∴直线BD为;y=x-2,直线CD为:y=3x-12,
∵直线l⊥CD,
∴直线l的解析式为:y=-
| 1 |
| 3 |
把D(5,3)代入得:b=
| 14 |
| 3 |
∴直线l的解析式为:y=-
| 1 |
| 3 |
| 14 |
| 3 |
∴A(0,
| 14 |
| 3 |
∴直线AC为:y=-
| 7 |
| 6 |
| 14 |
| 3 |
解;
|
|
∴F(
| 40 |
| 13 |
| 14 |
| 13 |
∴
| AF |
| FC |
| ||||
|
| 10 |
| 3 |
点评:本题考查了用待定系数法求二次函数和一次函数的解析式、二次函数和一次函数与坐标轴交点的问题以及两条直线交点的问题、相似三角形的判定和性质,题目的综合性较强,难度不小,特别是对学生的计算能力要求很高,是一道不错的中考压轴题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在实数0,
,
,
,π,
中,无理数一共有( )
| 2 |
| 5 |
| 7 |
| 3 | 4 |
| 25 |
| A、1个 | B、2个 | C、3个 | D、4个 |
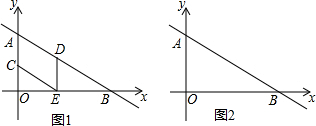 如图,在平面直角坐标系中,直线y=-
如图,在平面直角坐标系中,直线y=-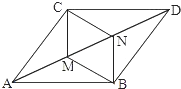 如图,?ABDC中,BN⊥AB,交AD于点N,CM⊥CD,交AD于点M,连接BM、CN
如图,?ABDC中,BN⊥AB,交AD于点N,CM⊥CD,交AD于点M,连接BM、CN 已知:如图,∠D=110°,∠EFD=70°,∠1=∠2.求证:∠3=∠B.
已知:如图,∠D=110°,∠EFD=70°,∠1=∠2.求证:∠3=∠B.