题目内容
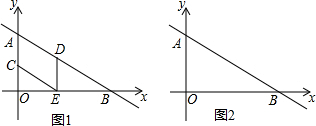 如图,在平面直角坐标系中,直线y=-
如图,在平面直角坐标系中,直线y=-
| ||
| 3 |
(1)①直接写出∠ABO的度数为
②证明在C、D运动过程中,四边形ACED是平行四边形.
(2)当t=
(3)连接DC,当t为何值时,△DEC为直角三角形?
考点:一次函数综合题
专题:
分析:(1)根据直线的斜率即可求得∠ABO=30°,根据30°所对的直角边等于斜边的一半即可求得DE=AC=t,从而证得四边形ACED是平行四边形.
(2)根据邻边相等的平行四边形是菱形得出AD-DB=DE=t,从而求得t的值;
(3)若△DEC为直角三角形,则CD∥OB,从而得出
=
,即
=
,得出t的值;
(2)根据邻边相等的平行四边形是菱形得出AD-DB=DE=t,从而求得t的值;
(3)若△DEC为直角三角形,则CD∥OB,从而得出
| AC |
| OA |
| AD |
| AB |
| t |
| 6 |
| 12-2t |
| 12 |
解答:(1)解:①∵直线y=-
x+6的斜率为-
,
∴∠ABO=30°;
②证明:在RT△BFD中,BD=2t,∠ABO=30°,
∴DE=
BD=t,
∵AC=t,
∴AC=DE,
又∵AC∥DE,
∴四边形ACED是平行四边形.
(2)解:∵由直线y=-
x+6可知OA=6,∠ABO=30°,
∴AB=2OA=12,
∵若四边形ACED是菱形,则AD=DE=t,
∴AD-DB=DE=t,
即12-2t=t,解得:t=4,
所以当t=4时四边形ACED是菱形;
(3)解:当△DEC为直角三角形时,
①∠CDE=90°,
∵DE∥AO,∴∠ACD=90°,
∵∠A=60°,∴AD=2AC,
∵AD=12-2t,AC=t,
∴12-2t=2t,
解得t=3.
②∠DCE=90°,
∵AD∥CE,∴∠ADC=90°,
∵∠A=60°,∴AC=2AD,
即t=2(12-2t)
解得t=4.8
∴当t=3或4.8时,△DEC为直角三角形.
| ||
| 3 |
| ||
| 3 |
∴∠ABO=30°;
②证明:在RT△BFD中,BD=2t,∠ABO=30°,
∴DE=
| 1 |
| 2 |
∵AC=t,
∴AC=DE,
又∵AC∥DE,
∴四边形ACED是平行四边形.
(2)解:∵由直线y=-
| ||
| 3 |
∴AB=2OA=12,
∵若四边形ACED是菱形,则AD=DE=t,
∴AD-DB=DE=t,
即12-2t=t,解得:t=4,
所以当t=4时四边形ACED是菱形;
(3)解:当△DEC为直角三角形时,
①∠CDE=90°,
∵DE∥AO,∴∠ACD=90°,
∵∠A=60°,∴AD=2AC,
∵AD=12-2t,AC=t,
∴12-2t=2t,
解得t=3.
②∠DCE=90°,
∵AD∥CE,∴∠ADC=90°,
∵∠A=60°,∴AC=2AD,
即t=2(12-2t)
解得t=4.8
∴当t=3或4.8时,△DEC为直角三角形.
点评:本题考查了有一个角是30°的直角三角形的性质,平行四边形的判定,菱形的判定以及平行线分线段成比例定理,熟练掌握直角三角形的性质,平行四边形的性质,菱形的性质是本题的关键;

练习册系列答案
相关题目
一个直角三角形的两条直角边分别为5、12,则第三边长为( )
| A、13 | ||
B、13或
| ||
C、
| ||
| D、7 |
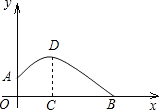 如图,一个运动员推铅球,铅球在点A处出手,出手时球离地面约1.8m.铅球落地点在B处,铅球运行中在运动员前3m处(即OC=3)达到最高点,最高点高为3.6m.已知铅球经过的路线是抛物线,根据图示的直角坐标系,你能算出该运动员的成绩吗?
如图,一个运动员推铅球,铅球在点A处出手,出手时球离地面约1.8m.铅球落地点在B处,铅球运行中在运动员前3m处(即OC=3)达到最高点,最高点高为3.6m.已知铅球经过的路线是抛物线,根据图示的直角坐标系,你能算出该运动员的成绩吗?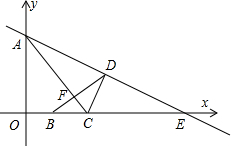 已知抛物线
已知抛物线 如图,一个四边形纸片ABCD,∠B=∠D=90°,把纸片按如图所示折叠,使点B落在AD边上的B′点,AE是折痕,∠C=130°,则∠AEB的度数为
如图,一个四边形纸片ABCD,∠B=∠D=90°,把纸片按如图所示折叠,使点B落在AD边上的B′点,AE是折痕,∠C=130°,则∠AEB的度数为