题目内容
【题目】如图,矩形![]() 中,
中,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,将
,将![]() 沿
沿![]() 折叠,点
折叠,点![]() 的对应点为
的对应点为![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,且
,且![]() ,在
,在![]() 边上有一点
边上有一点![]() ,使得
,使得![]() 的值最小,此时
的值最小,此时![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
设BD与AF交于点M.设AB=a,AD=![]() a,根据矩形的性质可得△ABE、△CDE都是等边三角形,利用折叠的性质得到BM垂直平分AF,BF=AB=a,DF=DA=
a,根据矩形的性质可得△ABE、△CDE都是等边三角形,利用折叠的性质得到BM垂直平分AF,BF=AB=a,DF=DA=![]() a.解直角△BGM,求出BM,再表示DM,由△ADM∽△GBM,求出a=2
a.解直角△BGM,求出BM,再表示DM,由△ADM∽△GBM,求出a=2![]() ,再证明CF=CD=2
,再证明CF=CD=2![]() .作B点关于AD的对称点B′,连接B′E,设B′E与AD交于点H,则此时BH+EH=B′E,值最小.建立平面直角坐标系,得出B(3,2
.作B点关于AD的对称点B′,连接B′E,设B′E与AD交于点H,则此时BH+EH=B′E,值最小.建立平面直角坐标系,得出B(3,2![]() ),B′(3,-2
),B′(3,-2![]() ),E(0,
),E(0,![]() ),利用待定系数法求出直线B′E的解析式,得到H(1,0),然后利用两点间的距离公式求出BH=4,进而求出
),利用待定系数法求出直线B′E的解析式,得到H(1,0),然后利用两点间的距离公式求出BH=4,进而求出![]() =
=![]() .
.
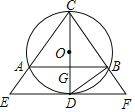
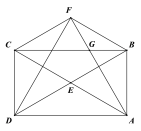
如图,设BD与AF交于点M.设AB=a,AD=![]() a,
a,

∵四边形ABCD是矩形,
∴∠DAB=90°,tan∠ABD=![]() ,
,
∴BD=AC=![]() =2a,∠ABD=60°,
=2a,∠ABD=60°,
∴△ABE、△CDE都是等边三角形,
∴BE=DE=AE=CE=AB=CD=a,
∵将△ABD沿BD折叠,点A的对应点为F,
∴BM垂直平分AF,BF=AB=a,DF=DA=![]() a,
a,
在△BGM中,∵∠BMG=90°,∠GBM=30°,BG=2,
∴GM=![]() BG=1,BM=
BG=1,BM=![]() GM=
GM=![]() ,
,
∴DM=BD-BM=2a-![]() ,
,
∵矩形ABCD中,BC∥AD,
∴△ADM∽△GBM,
∴![]() ,即
,即![]() ,
,
∴a=2![]() ,
,
∴BE=DE=AE=CE=AB=CD=2![]() ,AD=BC=6,BD=AC=4
,AD=BC=6,BD=AC=4![]() ,
,
易证∠BAF=∠FAC=∠CAD=∠ADB=∠BDF=∠CDF=30°,
∴△ADF是等边三角形,
∵AC平分∠DAF,
∴AC垂直平分DF,
∴CF=CD=2![]() ,
,
作B点关于AD的对称点B′,连接B′E,设B′E与AD交于点H,则此时BH+EH=B′E,值最小.
如图,建立平面直角坐标系,

则A(3,0),B(3,2![]() ),B′(3,-2
),B′(3,-2![]() ),E(0,
),E(0,![]() ),
),
易求直线B′E的解析式为y=-![]() x+
x+![]() ,
,
∴H(1,0),
∴BH=![]() =4,
=4,
∴![]() =
=![]() .
.
故选:B.

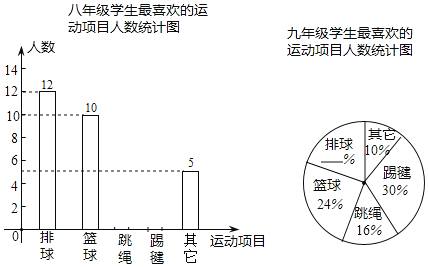
【题目】通辽市某中学为了了解学生“大课间”活动情况,在七、八、九年级的学生中,分别抽取了相同数量的学生对“你最喜欢的运动项目”进行调查(每人只能选一项),调查结果的部分数据如下表(图)所示,其中七年级最喜欢跳绳的人数比八年级多5人,九年级最喜欢排球的人数为10人.
七年级学生最喜欢的运动项目人数统计表
项目 | 排球 | 篮球 | 踢毽 | 跳绳 | 其他 |
人数(人) | 7 | 8 | 14 |
| 6 |
请根据以上统计表(图)解答下列问题:
(1)本次调查共抽取了多少人?
(2)补全统计表和统计图.
(3)该校有学生1800人,学校想对“最喜欢踢毽子”的学生每4人提供一个毽子,学校现有124个毽子,能否够用?请说明理由.